Необходимое и достаточное условие сходимости ряда (Критерий Коши)

Определение

Ряд 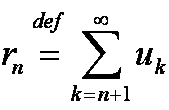называется n-ым остатком ряда.

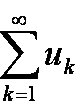Следствие 2

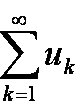Последовательность остатков сходящегося ряда является бесконечно малой.

Доказательство

Если ряд 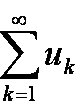сходится, то из условия Коши, взятого со значением , при переходе m → ∞ получим,  что

⇔

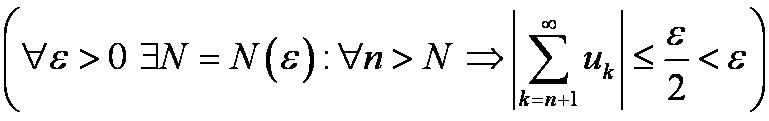(∀ ε > 0 ∃ N = N (ε): ∀ n > N ⇒ |r_n| < ε) ⇔ .