Необходимое и достаточное условие сходимости ряда (Критерий Коши)

Пример

Гармонический ряд

Рассмотрим ряд 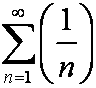. Для него выполнено необходимое условие сходимости: 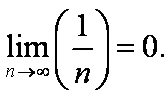Однако, согласно критерию Коши, этот ряд расходится. В самом деле,  отрицание условия Коши имеет вид:

∃ ε > 0: ∀ N ∃m > n > N: 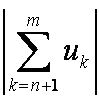≥ ε

Возьмём , рассмотрим любое N, и пусть n = N + 1, m = 2N + 2

Очевидно, m > n > N.

Тогда

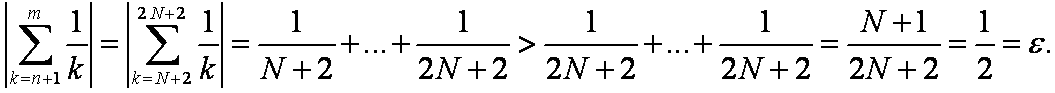
Таким образом,

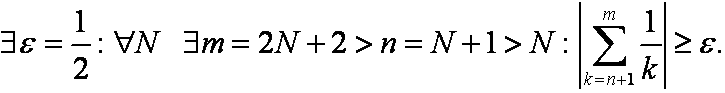Ряд расходится.