Признаки Раабе и Гаусса
Теорема
Признак Раабе в допредельной форме
Если существует число r > 1, такое что, начиная с некоторого номера n0 выполнено неравенство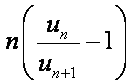 
≥ r,
то ряд 
сходится, если же для n > n0 ⇒ 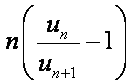≤ 1, то ряд расходится.
Теорема
Признаки Раабе и Гаусса
Если существует 
= r, то при r > 1 ряд сходится, если же r < 1, то ряд расходится.
Теорема
Признак Гаусса
Если существуют числа α, λ, μ > 0 и ограниченная последовательность {ϑn}, такие что, начиная с некоторого номера n0 выполнено равенство 
то при λ > 1 ряд сходится, а при λ < 1, он расходится, если же λ = 1, то при
μ > 1 ряд сходится, а при μ ≤ 1, он расходится.
22/28
