Числовые ряды
1. Ограниченность фундаментальной последовательности
Пусть последовательность {zk} фундаментальна. То есть
∀ ε > 0 ∃ N ∈ |
(1.8) |
: ∀ n > N ∀ p ∈ 
|zn+p − zn| < εОтсюда все числа zk при k ≥ N находятся в ε–окрестностях числа zN+1. Поэтому все элементы последовательности zn ограничены по модулю числом
max {|z1|, ..., |zN|; |zN+1| + ε}.
2. Теорема Больцано–Вейерштрасса
Докажем, что у любой ограниченной последовательности существует сходящаяся подпоследовательность. В самом деле, пусть все элементы последовательности {zk} находятся в прямоугольнике П1 = {z = a + ib: a ∈ [p, q], b ∈ [r, s]} на плоскости 
. Выберем любой элемент последовательности в прямоугольнике и назовём его 
— первым элементом подпоследовательности. Поделим П1 на 4 равных прямоугольника отрезками, соединяющими середины противоположных сторон. В один из прямоугольников наверняка попадёт бесконечное число элементов последовательности. Обозначим его П2. Выберем в П2 любой элемент последовательности и назовём его 
— вторым элементом подпоследовательности. Это прямоугольник мы также разделим на 4 равных прямоугольника и будем продолжать это процесс до бесконечности. Таким образом, мы получим подпоследовательность {
}, причём ∀ m ∈ 
∈ Пm. Но последовательность проекций сторон Пm на ось Ox есть последовательность стягивающихся отрезков, поэтому имеет только одну общую для всех отрезков точку P. Аналогично, последовательность проекций Пm на ось Oy имеет одну общую для всех отрезков точку R. Таким образом, существует ровно одна точка, общая для всех прямоугольников Пm:
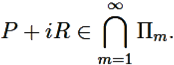
Эта точка и является пределом подпоследовательности {
}, поскольку все члены этой подпоследовательности, начиная с номера N находятся в прямоугольнике ПN, размеры которого в 2N−1 раз меньше, чем размеры П.
