Числовые ряды

Абсолютная сходимость

Определение 1.5

Если сходится ряд из модулей |z_k| сходится, то числовой ряд z_k называется абсолютно сходящимся.

Утверждение 1.1

Условие

|z_k| сходится.

Утверждение

z_k сходится.

Доказательство

По критерию Коши сходимости числового ряда, из уловия теоремы следует:

∀ ε > 0   ∃ N ∈ : ∀ n > N   ∀ p ∈  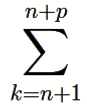  |z_k| < ε.

Оценим сумму:

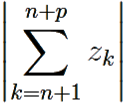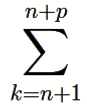≤ |z_k| < ε.

Поэтому, для ряда 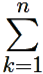z_k также выполнено условие критерия Коши, следовательно, он сходится.