Функции комплексного переменного

Пример 2.1

Функция = z² определена на всей комплексной плоскости и является однозначной, т. к. каждому числу z = re^iφ ставит в соотвествие ровно одно число = r²e^i·2φ.

В то же время, функция z = является двузначной, ибо если рассмотреть показательную форму записи числа
= ρe^{i(θ + 2πk)}, т. е. записать вместо arg = θ многозначный Arg = θ + 2πk, k ∈ , то извлечение корня из даёт:

Таким образом, каждому комплексному числу соответствует два различных корня из :

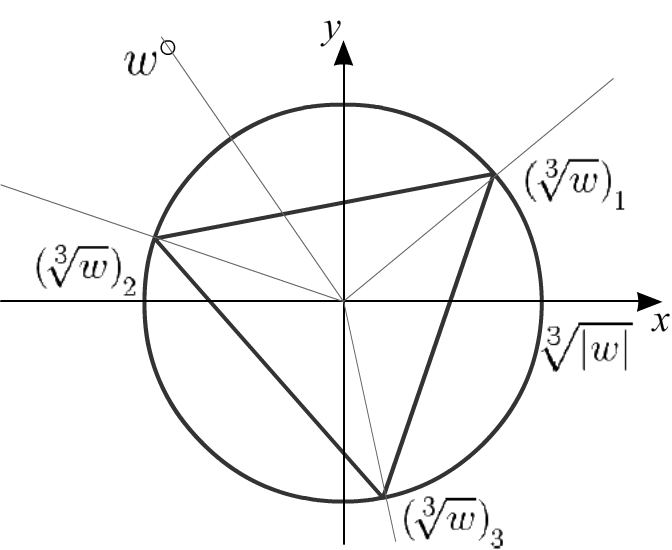
Аналогично, функция является n-значной, При этом все n различных корней располагаются на комплексной плоскости на окружности с центром в начале координат и являются вершинами правильного n-угольника.