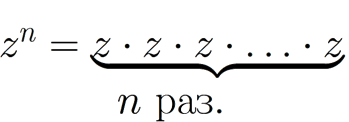Комплексные числа и действия над ними

Определение 1.2

Пусть z₁ = a₁ + ib₁ и z₂ = a₂ + ib₂.

z₁ = z₂   ⇔   a₁ = a₂,   и   b₁ = b₂.

Число = a − ib называется комплексно сопряжённым к числу z = a + ib.

Операции сложения (вычитания), умножения, деления и возведения в натуральную степень n определяются следующим образом:

	z1 ± z2 = (a1 ± a2) + i(b1 ± b2),	(1.1)
	z1 · z2 = (a1a2 − b1b2) + i(a1b2 + a2b1),	(1.2)
	,	(1.3)
		(1.4)

Пример 1

Из определения операции умножения сразу получаем:

i² = (0·0 − 1·1) + i(0·1 + 1·0) = −1 + 0 · i = −1.

Пример 2
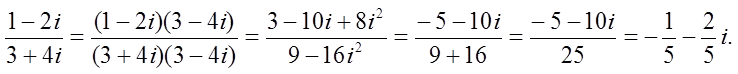
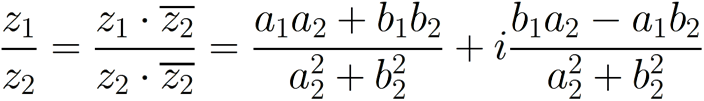