Комплексные числа и действия над ними

Формы записи комплексного числа

• z = a + ib,   a = Re z,   b = Im z — алгебраическая форма записи;
• z = r (cos φ + i sin φ),   r = |z|,   φ = arg z — тригонометрическая форма записи;
• z = re^iφ,   r = |z|,   φ = arg z — показательная форма записи.

Первые две формы записи комплексного числа легко получаются из геометрической интерпретации множества комплексных чисел как комплексной плоскости. Показательная (или экспоненциальная) форма получается из тригонометрической, если применить формулу Л. Эйлера:

Формула Л. Эйлера

e^iφ = cos φ + i sin φ.

Из неё также следуют ещё две важные формулы:

,   

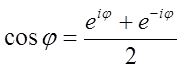Надо заметить, что при выполнении сложения удобна алгебраическая форма записи комплексных чисел, а при умножении, делении и возведении в степень часто удобнее показательная форма. В самом деле, пусть , а .

Тогда , а . Эти формулы и проще, чем если бы мы пользовались алгебраической формой записи, и имеют наглядную геометрическую интерпретацию:

— при умножении чисел их модули перемножаются,а аргументы складываются;

— при возведении числа в натуральную степень n ∈ его модуль возводится в степень n, а аргумент умножается на n.