Поведение в окрестности устранимой особой точки

Теорема 9.2

Обратная теорема

Условие

f(z) аналитична и ограничена |f(z)| < M в окрестности изолированной особой точки z = a.

Утверждение

Точка z = a — устранимая особая точка функции f(z).

Доказательство

Так как f(z) аналитична в окрестности изолированной особой точки z = a, то её можно разложить в ряд Лорана в кольце
{z: 0 < |z − a| < R}. Рассмотрим формулы вычисления коэффициентов ряда:

$$c_n = \frac{1}{2 \pi i} \int_{\gamma} \frac{f(\zeta)}{(\zeta - a)^{n+1}} d \zeta, $$

где контуром интегрирования γ является произвольная окружность с центром в z = a и радиусом ρ < R. Поскольку |f(z)| < M, то |c_n| < 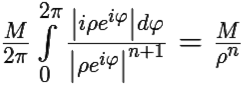. При этом, данная оценка верна сразу для всех окружностей γ радиусом ρ < R, поэтому в последнем неравенстве при n < 0 можно перейти к пределу при ρ → +0. Левая часть от γ, то есть от ρ, не зависит, следовательно, не изменится, а правая при n < 0 стремится к 0. Поэтому c_n = 0 при n < 0.