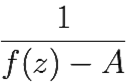Поведение функции в окрестности существенно особой точки

Теорема 9.4

Сохоцкого–Вейерштрасса

Условие

f(z) аналитична в окрестности существенно особой точки z = a.

Утверждение

∀ A ∈   ∀ ε > 0   ∀ δ > 0   ∃ z₁: |z₁ − a| < δ, в которой |f(z₁) − A| < ε.

Замечание 9.2

Эту теорему иногда формулируют иначе, заменяя её утверждение на

∀ A ∈   ∃ z_n = a,   f(z_n) → A, n → ∞.

Доказательство

Пусть утверждение теоремы неверно, то есть

∃ A ∈   ∃ ε > 0   ∃ δ > 0:   ∀ z: |z − a| < δ верно неравенство |f(z) − A| ≥ ε.

Тогда функция

(z) =

(9.1)

определена, аналитична и ограничена в {z: 0 < |z − a| < δ}.