Изолированные особые точки и их классификация. Примеры

Пример 9.1

Устранимая особая точка.

Рассмотрим функцию f(z) = в окрестности точки a = 0. По определению функции sin z

sin z =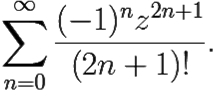

Отсюда,

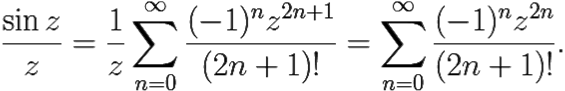
Как видим, данный ряд Лорана (сходящийся всюду в ) не содержит слагаемых с отрицательными степенями z. Поэтому, точка
a = 0 (значение f(z) в ней не определено) является УОТ.

Легко, кстати, найти предел этой функции в точке a = 0:

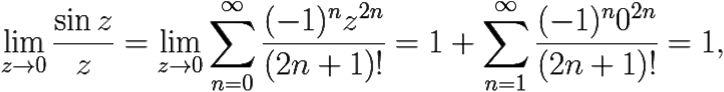
то есть на комплексной плоскости также имеет место Первый Замечательный Предел: