Изолированные особые точки и их классификация. Примеры

Пример 9.2

Плюс порядка k.

Пусть k ∈ . Тогда функция f(z) = имеет в точке z = a плюс порядка k.

В самом деле, её ряд Лорана в окрестности этой точки содержит ровно 1 слагаемое и имеет вид:

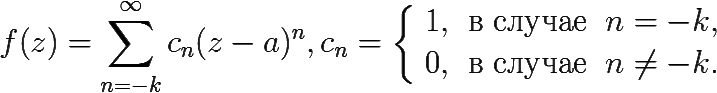
Таким образом, для f(z) выполнено определение ППk в точке z = a.

Пример 9.3

Существенно особая точка.

Рассмотрим функцию f(z) = в окрестности z = 0. Её ряд Лорана выглядит так:

$$ e^{-\frac{1}{z}} = \left [ y = -\frac{1}{z} \right ] = \sum_{n=0}^{\infty} \frac{y^n}{n!} = \sum_{n=0}^{\infty} \frac{-1}{z^n \cdot n!} = \left [ k = -n \right ] = \sum_{k = - \infty}^{0} \frac{-1^k z^k}{(-k)!}, $$

Таким образом, ряд Лорана f(z) содержит бесконечное число слагаемых при отрицательных степенях z , следовательно, точка z = 0 — СОТ функции .