Вычеты

Вычет в z = ∞

Несколько забегая вперёд, приведём определение и формулы для вычисления вычета в точке z = ∞.

Определение 10.2

Вычетом функции f(z) в изолированной особой точке z = ∞ называется число, равное:

Res f(∞) = 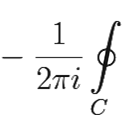f(ζ)dζ = −c₋₁,

где интеграл берётся в положительном направлении по произвольному замкнутому контуру C, во внешности которого нет других особых точек, а c₋₁ — коэффициент при z⁻¹ ряда Лорана функции f(z) в кольце {r < |z| < ∞}.

Для вычисления вычета в точке z = ∞ есть три способа:

• первый:

Res f(∞) = [− zf(z)],  если этот предел существует;

(10.4)



• второй: разложить функцию в ряд Лорана в любом кольце {r < |z| < ∞} и взять коэффициент c₋₁ с обратном знаком;


• третий: воспользоваться основной теоремой о вычетах (см. следующий пункт).