Вычеты
Вычет в полюсе порядка k
Пусть точка a является полюсом порядка k функции f(z). Это значит, что её ряд Лорана в окрестности данной точки имеет вид:
f(z) = ![]() + c0 + c1(z − a) + ... .
+ c0 + c1(z − a) + ... .
Умножив обе части на (z − a)k, получим:
(z − a)kf(z) = c−k + c−k+1(z − a) + ... + c−2(z − a)k−2 + c−1(z − a)k−1 + ... .
Возьмём от обеих частей производную порядка (k − 1), чтобы обнулить все слагаемые от c−k до c−2(z − a)k−2 и перейдём в полученном равенстве к пределу при z → a, чтобы обнулились все слагаемые, начиная с c0. Получим:
Res f(a) = |
(10.3) |
Как легко заметить, формула (10.1) является частным случаем (10.3) при k = 1.
Вычет в существенной особой точке
Для вычета в существенно особой точке простых формул нет. Поэтому его надо считать либо по определению, как интеграл, либо при помощи разложения в ряд Лорана, чтобы найти c−1.


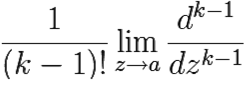 [(z − a)kf(z)], k = 1, 2, 3...
[(z − a)kf(z)], k = 1, 2, 3... 
