Вычеты

Вычет в полюсе первого порядка

Пусть z = a — полюс первого порядка f(z). Тогда ряд Лорана f(z) в окрестности z = a имеет вид:

f(z) = + c₀ + c₁(z − a) + ...

Умножим обе части на (z − a) и перейдём в полученном равенстве к пределу при z → a:

Есть и другая формула для вычисления вычета в полюсе первого порядка.

Пусть

f(z) = ,   φ(a) ≠ 0,

а ψ(z) имеет в z = a нуль первого порядка, то есть представима в виде

ψ(z) = ,   ψ′(a) ≠ 0.

Тогда (z − a)f(z) = (z − a)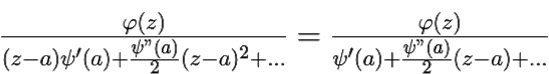 и, переходя к пределу при z → a, по формуле (10.1) получим: