Вычеты
Доказательство
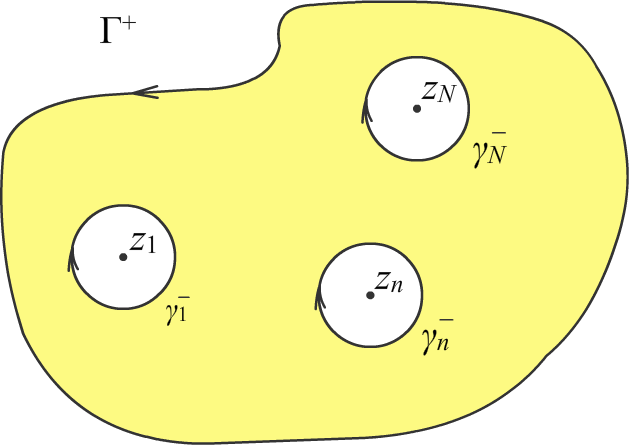
Вырежем каждую из особых точек an замкнутым контуром γn так, чтобы он не пересекал ни Г+, ни другие контура γk. Рассмотрим многосвязную область D*, ограниченную контурами Г+ и γn, n = 1, 2, ... , N . Внутри указанной области функция f(z) не имеет особых точек, то есть она везде аналитична, в том числе и на границе ∂D* этой области.
|
Поэтому, по Интегральной Теореме Коши, интеграл от f(z) по ∂D*, проходимой в положительном направлении, равен нулю.
А из чего состоит граница ∂D*? Из контура Г+ и объединения контуров γn−, проходимых по часовой стрелке.
|
Перенеся теперь сумму интегралов по γn− в правую часть и поменяв направление обхода на положительное, получим
|
(10.5) |
А так как 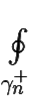 f(z)dz = 2πi Res f(an), то утверждение теоремы доказано.
f(z)dz = 2πi Res f(an), то утверждение теоремы доказано.


 f(z)dz = 0
f(z)dz = 0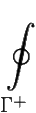 f(z)dz +
f(z)dz + 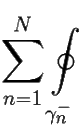 f(z)dz = 0
f(z)dz = 0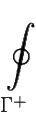 f(z)dz =
f(z)dz = 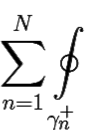 f(z)dz
f(z)dz
