Вычеты

Теперь предположим, что за пределами односвязной области D функция f(z) не имеет особенностей, тогда определён вычет f(z) в точке z = ∞:

Res f(∞) = 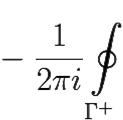f(ζ)dζ = −c₋₁.

Поэтому формулу (10.5) можно переписать в виде:

−2πi Res f(∞) = 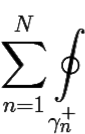f(z)dz

или

2πi Res f(∞) + 2πi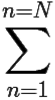 Res f(a_n) = 0.

Этот результат сформулирован в виде теоремы:

Теорема 10.2

Условие

f(z) аналитична всюду в , за исключением конечного числа изолированных особых точек и точки a₀ = ∞.

Утверждение

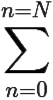Res f(a_n) = 0.