Вычеты

Вычисление контурных интегралов с помощью вычетов

Пример 11.1

Вычислить интеграл: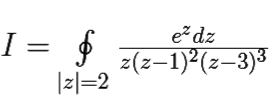

Заметим, в первую очередь, что внутрь контура интегрирования попадают только две особые точки подынтегральной функции: z₀ = 0 и z₁ = 1 , поскольку z₂ = 3 лежит во внешности контура C = {|z| = 2}. Поэтому, в силу основной теоремы о вычетах,

dz = 2πi(Res f(0) + Res f(1)).

Вычислим вычеты. Очевидно, z₀ = 0 — полюс первого порядка, а z₁ = 1 — полюс второго порядка. Поэтому, по формулам (10.1) и (10.3), получаем:

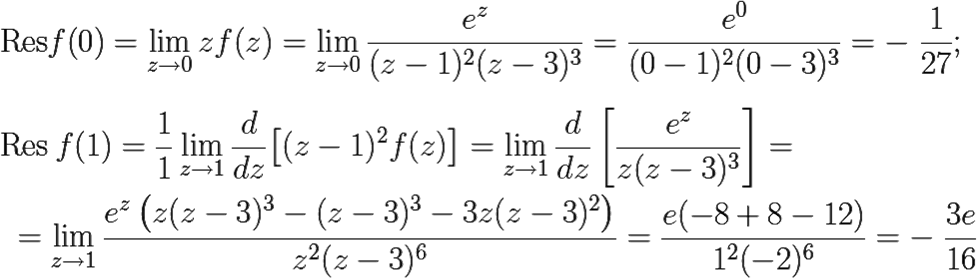
Таким образом,
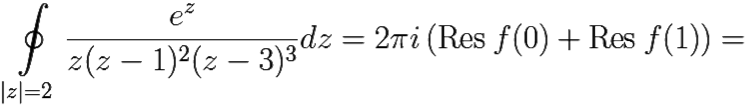