Лемма Жордана и несобственные интегралы

Доказательство

Нам дано, что f(z) 0 при z → ∞, Im z > 0 равномерно относительно arg z. Это означает, что при |z| = R имеет место оценка

|f(z)| < µ(R),   |z| = R,  где µ(R) → 0 при R → +∞.

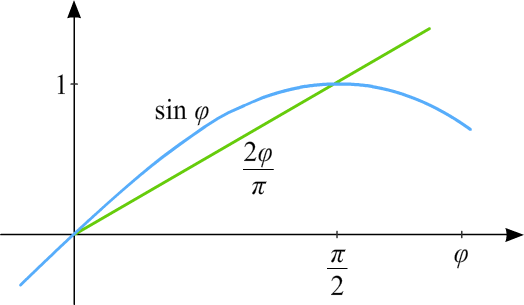
Кроме этой оценки нам потребуется очевидное из рисунка соотношение

sin φ ≥ φ при φ ∈ [0, ].