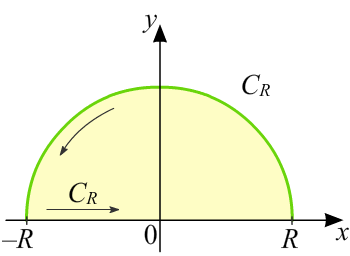
Лемма Жордана и несобственные интегралы

Пример 11.2

Вычислить интеграл I = 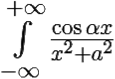dx, α, a > 0.

В силу формулы Эйлера, I = Re I₁ = Re 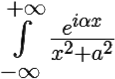dx.

Рассмотрим функцию комплексной переменной

f(z) .

Она удовлетворяет требованиям Леммы Жордана:

1) f(z) аналитична в верхней полуплоскости Im z > 0, за исключением конечного числа изолированных особых точек . В данном случае особая точка в верхней полуплоскости только одна z₁ = ia, и она является полюсом первого порядка.