Лемма Жордана и несобственные интегралы

2) f(z) 0 при z → ∞, Im z > 0 равномерно относительно arg z.

Поэтому

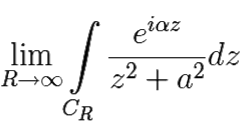= 0.

Представим главное значение искомого интеграла I₁ (если он сходится, то обязательно к своему главному значению) в виде:

I₁ = ,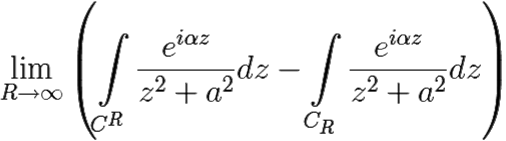

где C^R — замкнутый контур, состоящий из отрезка действительной оси [−R, R] и полуокружности C_R. При достаточно больших R интеграл по замкнутому контуру можно вычислить по основной теореме о вычетах: пусть F(z) = e^iαzf(z), тогда:

F(z) = e^iαzf(z)

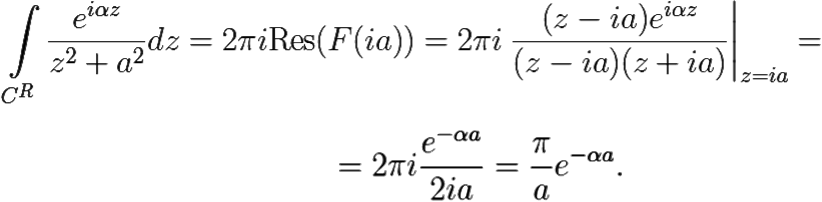
Поэтому

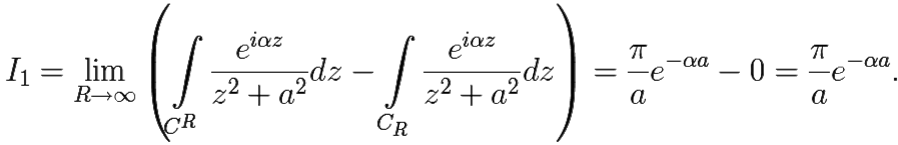
И, наконец, т. к. I = Re I₁, то I = Re