Изолированные особые точки
Так же, как и для конечной изолированной особой точки, здесь возможны три случая:
Определение 9.3
Изолированная особая точка z = ∞ функции f(z) называется
- устранимой особой точкой функции f(z), если её ряд Лорана в кольце {z: R < |z| < ∞} не содержит слагаемых с положительными номерами:
f(z) = ![]() cnzn =
cnzn = ![]()
- полюсом порядка k функции f(z), если её ряд Лорана в кольце {z: R < |z| < ∞} содержит слагаемое с положительным номером k и не содержит слагаемых с номерами, большими k:
- существенно особой точкой функции f(z), если её ряд Лорана в кольце {z: R < |z| < ∞} содержит бесконечное число слагаемых с положительными номерами:
f(z) = 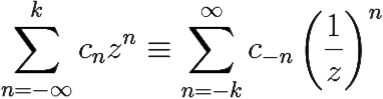 , ck ≠ 0.
, ck ≠ 0.
f(z) = ![]() cnzn
cnzn
и ∀ N ∈ ![]() ∃ n > N: cn ≠ 0.
∃ n > N: cn ≠ 0.



