Изолированные особые точки

Пример 9.7

Функция f(z) = аналитична всюду, кроме точки z = 0 и, быть может, точки z = ∞ (последнюю всегда следует проверять отдельно). Чтобы выяснить характер особенностей сразу в обеих точках z = 0 и z = ∞ , напишем ряд Лорана f(z) в кольце
0 < |z| < ∞:

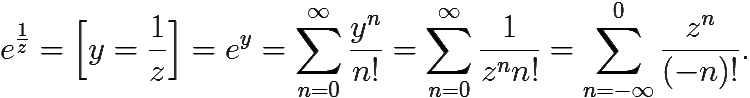
Как мы видим, данный ряд содержит бесконечное число слагаемых с отрицательными степенями z и не содержит ни одного слагаемого с положительной степенью z. Поэтому, в силу определений типов изолированных особых точек, точек z = 0 является существенно особой, а z = ∞ — устранимой особой точкой функции f(z) = .