Преобразование Лапласа

Доказательство

1) cразу следует из свойства линейности интеграла.

2) f(λt)

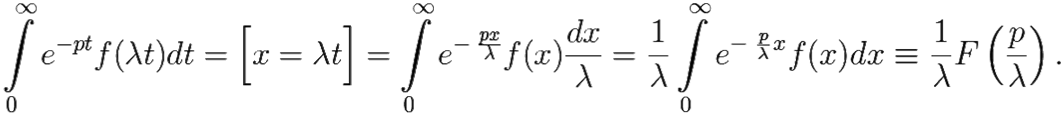
3) Пусть f(t) F(p) и возьмём сначала n = 1. Тогда:

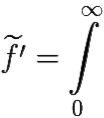e^−pt f′(t)dt = [по частям] = e^−pt f(t) 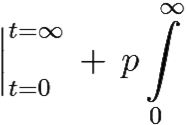e^−pt f(t)dt= −f(0) + pF(p).

Здесь мы воспользовались тем, что |e^−pt f(t)| ≤ M|e^−pt|e^αt = Me^{(α−Re p)t}. |e^{−i Im p·t}| = Me^{(α−Re p)t}, откуда при всех

p ∈ : Re p > α имеем: e^−pt f(t) = 0. Таким образом,

F₁(p) = pF(p) − f(0).

Но, аналогично рассуждая, для производной f ″ функции f ′, получим

F₂(p) = pF₁(p) − f ′(0) ≡ p²F(p) − pf(0) − f ′(0).

Теми же рассуждениями мы за n шагов получим формулу для изображения функции f⁽ⁿ⁾:

f⁽ⁿ⁾t pⁿF(p) − pⁿ⁻¹f(0) − pⁿ⁻²f ′(0) − ... − pf⁽ⁿ⁻²⁾(0) − f⁽ⁿ⁻¹⁾(0).