Применение преобразования Лапласа к решению дифференциальных уравнений

Пример 12.2

Решить преобразованием Лапласа задачу Коши:

y″ + y′ = x − 1, y(0) = − 1, y′(0) = 1.

Пусть y(x) Y(p). Тогда, по свойству 3, y″ p²Y(p) − py(0) − y′(0).

В силу данных Коши y(0) = −1, y′(0) = 1, левая часть уравнения имеет изображение:

y″ + y p²Y(p) + Y(p) + p − 1 = (p² + 1)Y(p) + p − 1.

С другой стороны, правая часть (см. п. 3 и 1 таблицы), имеет изображение:

x − 1

Из двух последних соотношений получаем:

(p² + 1)Y(p) + p − 1 = ,

откуда

Y(p) =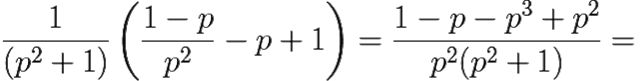

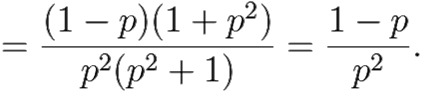
Таким образом, Y(p) = . Возвращаясь к таблице изображений, пункты 1 и 3, видим, что

y(x) = x − 1 .

Таким образом, данная задача Коши имеет решение y(x) = x − 1, а в силу единственности решения задачи Коши, других решений у неё нет.