Критерий Коши сходимости функционального ряда

Теорема 3.1

Критерий Коши сходимости функционального ряда

Утверждение

φ_k(z) сходится в D ⊆ ⇔ ∀ z ∈ D   ∀ ε > 0   ∃ N ∈ : ∀ n > N   ∀ p ∈

выполняется неравенство 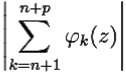< ε.

Доказательство

Фиксируем произвольную точку z ∈ D. Ряд φ_k(z), рассматриваемый в этой точке, является числовым рядом. По критерию Коши сходимости числового ряда, сходимость ряда в этой точке z ∈ D равносильна выполнению условия:

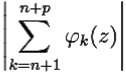∀ ε > 0   ∃ N ∈ : ∀ n > N   ∀ p ∈     < ε.