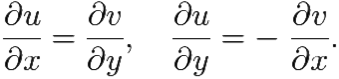Аналитические функции

Производная функции комплексного переменного

Определение 4.1

Число f ′(z₀) мы будем называть производной функции f(z) в точке z₀, если:

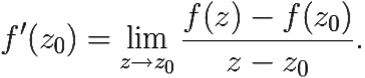
Саму функцию f(z) в случае, если этот предел существует, мы будем называть дифференцируемой в точке z₀.

Необходимое и достаточное условие дифференцируемости функции

Теорема 4.1

Условия Коши–Римана

Условие

Функция ƒ(z) = ƒ(x + iy) = u(x, y) + iυ(x, y) определена в некоторой окрестности точки z₀ = x₀ + iy₀, причём в точке
(x₀, y₀) функции u(x, y), υ(x, y) дифференцируемы.

Утверждение

Функция ƒ(z) дифференцируема в точке z₀   ⇔