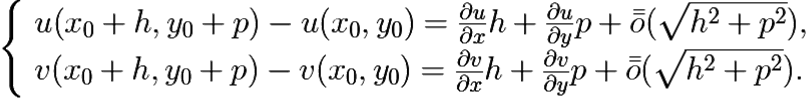Аналитические функции

⇐ (Достаточность)

Пусть z – z₀ = h + ip. В силу дифференцируемости функций u(x, y) и υ(x, y) как функций двух действительных переменных, по определению, имеем:

(4.1)

Отсюда,

или

Нам дано, что равенства выполнены. Поэтому

, и

Выражение — определённое число, не зависит от h + ip. Поделим полученное равенство на z – z₀ = h + ip, получим:

Таким образом существует число ƒ ′(z₀) = .