Аналитические функции

Следствие 4.1

Условие

ƒ(z) дифференцируема в точке z = z₀.

Утверждение

Для ƒ ′(z₀) верны формулы:

Пример 4.1

Рассмотрим функцию e^z = e^x+iy и выясним, в каких точках комплексной плоскости она является дифференцируемой. Для этого представим её в виде

e^z = e^x(cos y + i sin y) = e^x cos y + ie^x sin y = u(x, y) + iυ(x, y).

Проверим теперь выполнение условий Коши–Римана

Имеем:

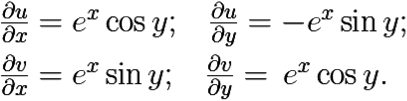
Очевидно, условия Коши–Римана выполняются при всех x, y ∈ и, следовательно, функция e^z является дифференцируемой в каждой точке z = x + iy ∈ .

То же самое верно и для функций sin z, cos z, sh z, ch z, т. к. они все являются суммами экспонент.