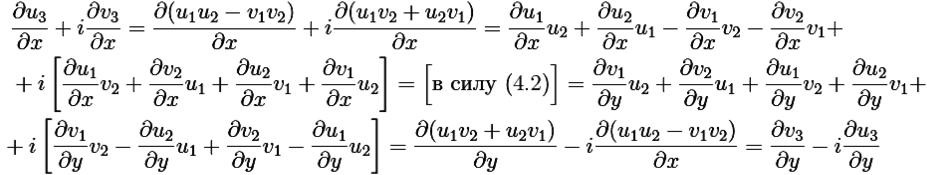Аналитические функции

Доказательство

По Теореме 4.1, аналитичность функции равносильна выполнению для неё условий Коши–Римана.
Поэтому для функций f(z) = u₁ + iυ₁ и (z) = u₂ + iυ₂ в области D справедливы равенства:

(4.2)

Покажем, например, что условия Коши–Римана выполнены и для f(z) · (z).

Рассмотрим

(4.3)

Равенство друг другу двух комплексных выражений возможно тогда и только тогда, когда совпадают их действительные и мнимые части соответственно. Поэтому (4.3) означает:

что и требовалось доказать. Аналитичность функций f(z) ± (z) и доказывается аналогично.