Дробно-линейная функция

Доказательство

1. В силу замечания 5.3, для проверки аналитичности дробно-линейной функции достаточно проверить аналитичность функций
₁(z) = z₀ + z₁z и ₂(z) = . Убедимся, что для этих функций выполнены условия Коши–Римана.

₁(z) = z₀ + z₁z = a₀ + ib₀ + (a₁ + ib₁)(x + iy) = (a₀ + a₁x − b₁y) + i(b₀ + a₁y + b₁x)

Во всей плоскости справедливы равенства:

Аналогично, рассмотрим ₂(z) = всюду в \z = 0:

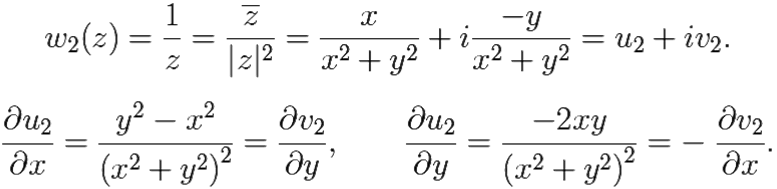
Таким образом, линейная функция и ₂ = аналитичны всюду, кроме точки, в которой знаменатель ₂ обращается в 0. Поэтому дробно-линейная функция f(z) = = λ аналитична в \{z = −β}.