Круговое свойство дробно-линейной функции
Определение 5.4
Окружностями на комплексной плоскости 
мы будем называть кривые, координаты точек которых удовлетворяют уравнению
A(x2 + y2) + Bx + Cy + D = 0, при некоторых A, B, C, D ∈ 
|A| + |B| + |C| + |D| ≠ 0.
Замечание 5.5
При таком определении под названием «окружность» попадают, кроме всех настоящих окружностей (для которых |A| ≠ 0, ещё и все прямые (для них А = 0, а |B| + |C| ≠ 0). Принято прямые называть окружностями бесконечного радиуса.
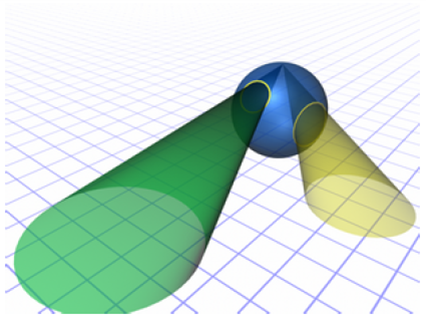
Естественность такого обобщения понятия окружности помогает проиллюстрировать сфера Римана (см. параграф 1.2 и рисунки): и прямые, и окружности, лежащие на плоскости z, имеют на сфере Римана своими образами окружности. Единственная разница между ними состоит в том, что образы прямых окружности, проходящие через «северный полюс», т. е. точку ∞, а образы обычных окружностей через ∞ не проходят.
|
|
