Гармонические функции

Теорема 4.3

Условие

Функции u(x, y), υ(x, y) ∈ C²(D).

Утверждение

f(z) = u(x, y) + iυ(x, y) — аналитическая функция в D    ⇔

⇔ u(x, y) и υ(x, y) — сопряжённые гармонические функции.

Доказательство

⇒ Из условия u, υ ∈ C²(D) следует, что смешанные производные этих функций не зависят от порядка дифференцирования, например, .

Убедимся, что Δu = 0 в D:

Δu = =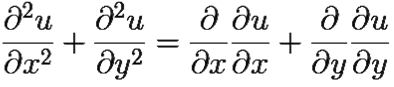

= [по условиям Коши–Римана] =

$$ = \frac{\partial}{\partial x} \frac{\partial \upsilon}{\partial y} - \frac{\partial}{\partial y} \frac{\partial \upsilon}{\partial x} = \frac{\partial^2 u}{\partial x \partial y} - \frac{\partial^2 \upsilon}{\partial y \partial x} = 0 $$

Тот факт, что Δ = 0 в D проверяется аналогично.

Условие 2) из определения сопряжённых гармонических функций сразу следует из аналитичности f(z) и Теоремы об условиях Коши–Римана.

⇐ Очевидным образом вытекает из Теоремы об условиях Коши–Римана.