Конформные отображения. Примеры

Осталось найти λ. Для этого у нас осталось неиспользованное условие соответствия границ: Im z = 0 || = 1. Воспользуемся им. Пусть z = x + iy, тогда на прямой Im z = 0 имеем z = x. Отсюда

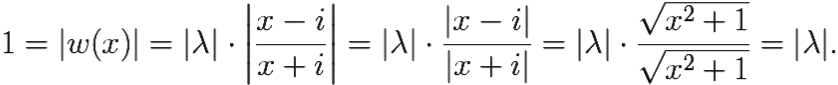
Итак, |λ| = 1.

Мы не нашли arg λ и не использовали условие arg (′(i)) = . Найдём ′(i):

Отсюда, . Следовательно,

Из условия arg (′(i)) = получаем: arg λ − = , откуда

arg (λ) = π.

Единственное число, модуль которого равен 1, а аргумент π — это число (−1). Таким образом, λ = −1.

Ответ

Например, = −.