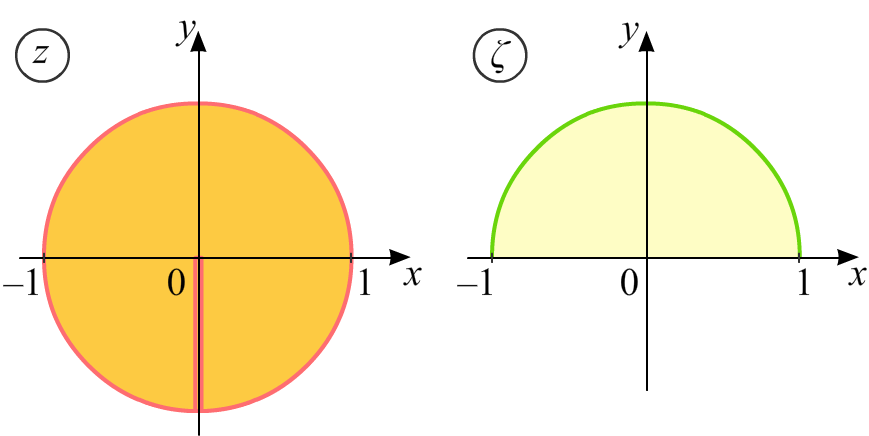Конформные отображения. Примеры

Пример 5.7

Найти конформное отображение круга |z| < 1 с разрезом по отрезку от точки z = 0 до точки z = −i на единичный круг || < 1.

Тут не удастся обойтись одной дробно-линейной функцией, иначе внутренность круга обязательно отобразилась бы во внутренность круга безо всяких разрезов.

Шаг 1

Поворот и перевод круга с разрезом в полукруг.

Во-первых, заметим, что круг с разрезом является «почти» двуугольником. В самом деле, границы этой фигуры есть дуги окружностей (одна из которых бесконечного радиуса). Но у этой фигуры, в отличие от двуугольников, во-первых, вершины совпадают z₁ = z₂ = −i, и, во-вторых, помимо углов при вершинах есть угол в 2π в середине «стороны», состоящей из двух отрезков [0, i].

Чтобы «выпрямить» эту строну, уменьшим угол в точке z = 0, равный 2π, в два раза при помощи операции извлечения квадратного корня, а чтобы «выпрямленная» сторона легла на ось Ox, совершим предварительный поворот на , домножив z на i = . ζ = ,  ветвь = 1. Ветвь корня = 1 была выбрана для того, чтобы полученный полукруг оказался в верхней полуплоскости.