Теорема о максимуме модуля

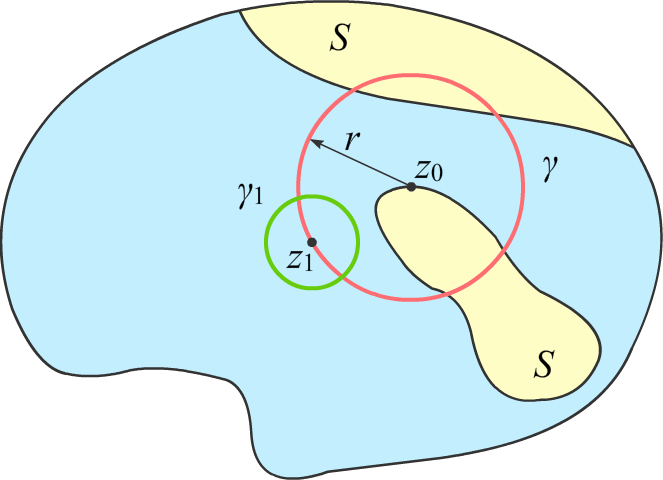
Проведём окружность γ с центром в z₀ радиуса r, достаточно малого, чтобы γ целиком лежала в D, и такую, чтобы на ней обязательно нашлась точка z₁ ∈ γ, в которой |f(z₁)| = m < M. (Это всегда возможно, ибо такие точки есть в любой окрестности z₀.)

Поскольку модуль непрерывной функции также непрерывна функция (проверить), то в некоторой окрестности точки z₁ всюду |f(z)| ≤ < M.

Пусть это неравенство выполнено на γ₁ — части окружности γ.