Ряд Тейлора
Теорема 7.2
Об аналитичности суммы ряда
Условие
∀ k ∈ 
fk(z) аналитичны в односвязной области D. Ряд 
fk(z) сходится равномерно в D.
Утверждение
Сумма ряда fk(z) аналитична в D.
Доказательство
Проинтегрируем данный ряд по любому замкнутому контуру C, целиком лежащему в D. По теореме 7.1, ряд можно интегрировать почленно:
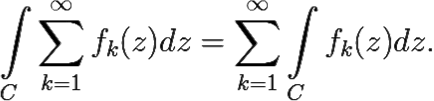
Но по интегральной теореме Коши 
fk(z)dz = 0 при всех k. Поэтому для любого замкнутого контура C ⊂ D
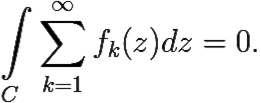
Непрерывность подынтегрального выражения следует из свойств равномерно сходящихся рядов функций действительной переменной (действительно, 
fk(z) = uk(x, y) + iυk(x, y), а uk и υk — непрерывные функции). Теперь мы имеем право применить теорему Морера непрерывная функция, интегралы от которой по всем замкнутым C ⊂ D равны нулю, является аналитической в D.
