Интеграл типа Коши
Теорема 6.7
Условие
С — произвольный ограниченный кусочно-гладкий контур, необязательно замкнутый, функция f(z) нeпрерывна на С, и функция F(z) при z ∉ C определена формулой
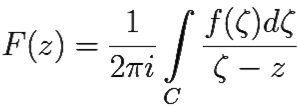 , z ∉ C.
, z ∉ C.
Утверждение
1) Функция F(z) аналитична в любой области, не содержащей точек контура С;
2) произвольные функции F(z) определяются формулами
|
(6.7) |
3) F(∞) = 0, причём F(z) = ![]() , z → ∞.
, z → ∞.
Замечание 6.2
Из данной теоремы о свойствах интеграла типа Коши можно получить совсем простое и короткое доказательство теоремы о бесконечной дифференцируемости аналитической функции. В самом деле, аналитическую в области функцию можно представить интегралом Коши по контуру C, лежащему в области аналитичности:
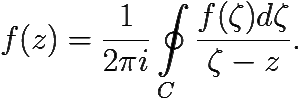
Интеграл в правой части частный случай интеграла типа Коши, поэтому, по тереме 6.7 f(z) бесконечно дифференцируема внутри C и её производные можно вычислить по формуле (6.6).


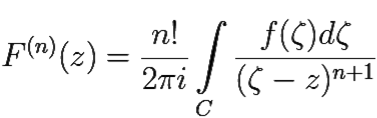 , z ∉ C, n = 0, 1, 2, ...; 1,
, z ∉ C, n = 0, 1, 2, ...; 1,
