Теорема Лиувилля

Теорема 6.8

Условие

f(z) аналитична всюду в и ограничена, т. е. ∃ M > 0: ∀ z ∈   |f(z)| ≤ M.

Утверждение

f(z) = const всюду в .

Доказательство

Поскольку f(z) аналитична в , для каждой точки z ∈ и окружности C радиуса R с центром в этой точке, верна интегральная формула Коши

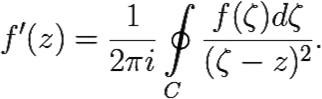
Оценим |f ′(z)|.

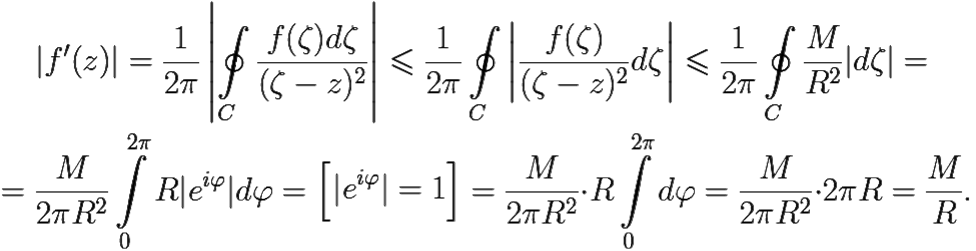
Итак, в каждой фиксированной точке z выполнено неравенство |f ′(z)| ≤ при любом R > 0. Устремим R → +∞. Так как левая часть не зависит от R, она не изменится, а правая стремится к нулю. Следовательно, в каждой точке z ∈ выполнено равенство |f ′(z)| = 0, откуда f(z) = const всюду в .