О радиусе сходимости степенного ряда

Найдём радиус сходимости ряда (z − z₀)^k+1.

По формуле Коши–Адамара:

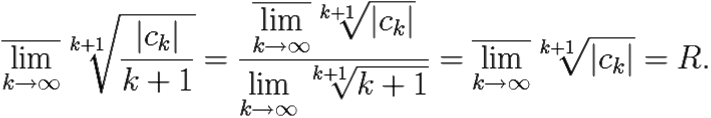
Таким образом, ряды (z − z₀)^k+1 и (z₁ − z₀)^k+1 сходятся абсолютно при |z − z₀| < R и |z₁ − z₀| < R. Поэтому их можно складывать (вычитать) почленно.

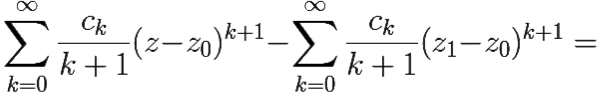
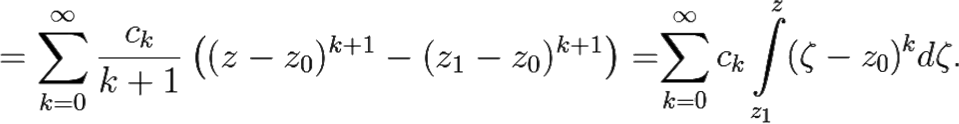
Поэтому данный ряд из интегралов на самом деле степенной. Наконец, поскольку вычитаемый ряд числовой и сходящийся, то радиус сходимости ряда c_k(ζ − z₀)^kdζ равен радиусу сходимости ряда (z − z₀)^k+1, а значит, и ряда

c_k(z − z₀)^k.