Вывод формулы суммы геометрической прогрессии

Выведем формулу суммы геометрической прогрессии для случая комплексных чисел.

Утверждение 7.1

Условие

q ∈ , q ≠ 1, n ∈ .

Утверждение

1 + q + q² + ... + qⁿ = .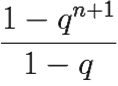

Доказательство

Обозначим сумму 1 + q + q² + ... + qⁿ через S_n.

Тогда с одной стороны:

1 + q + q² + ... + qⁿ + qⁿ⁺¹ = S_n + qⁿ⁺¹ ,

с другой стороны:

1 + q + q² + ... + qⁿ + qⁿ⁺¹ = 1 + q · S_n.

Сопоставляя эти два равенства, получаем

S_n + qⁿ⁺¹ = 1 + q · S_n.