Ряд Лорана

При k ≠ n этот интеграл равен

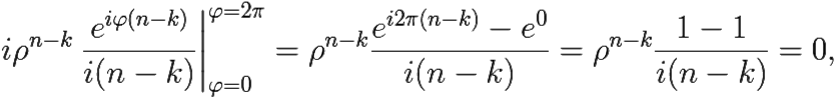
а при k = n он вычисляется так: iρ⁰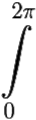1dφ = 2πi.

Таким образом,

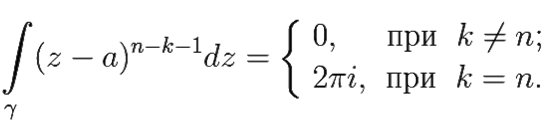
Поэтому из всех слагаемых правой части (8.8) останется только одно, не равное нулю, и

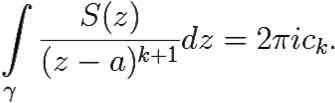
Данная формула совпадает с формулой вычисления коэффициентов ряда Лорана (8.2). А поскольку число k мы брали произвольным, то все коэффициенты заданного степенного ряда совпадают с коэффициентами ряда Лорана для функции S(z) в кольце {z: r < |z − a| < R}.

Замечание 8.1

Ряд Тейлора любой функции f(z), сходящийся к ней в некотором круге {z: |z − a| < R}, является также её рядом Лорана в кольце {z: 0 < |z − a| < R}. Действительно, раз функция разложима в ряд Тейлора в круге {z: |z − a| < R}, значит, она в нём аналитична. Поэтому в кольце {z: 0 < |z − a| < R} она также аналитична и, следовательно, представима рядом Лорана. При этом коэффициенты с номерами k ≥ 0 её ряда Лорана вычисляются по тем же формулам, что и коэффициенты ряда Тейлора. А коэффициенты ряда Лорана с номерами k < 0 все равны нулю, в силу интегральной теоремы Коши (теорема 6.3).