Ряд Лорана

Пример 8.2

Разложить функцию f(z) = (|a| < |b|) в степенной ряд в кольце |a| < |z| < |b|. Поскольку центр кольца точка

z = 0, то разложение f(z) должно быть по степеням z.

Шаг 1

Разложим данную функцию на простейшие дроби:

Шаг 2

Поскольку кольцо |a| < |z| < |b| есть пересечение внешности круга |z| ≤ |a| и внутренности круга |z| ≤ |b|, то первую дробь надо раскладывать в |z|> |a|, то есть по степеням .

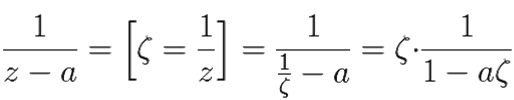= [по формуле Утв. 7.2] =

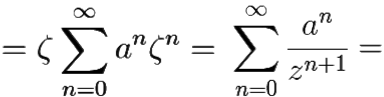
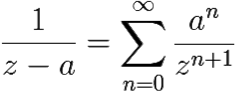= [переименуем индекс суммирования: k = n + 1] =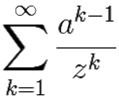

Поскольку мы воспользовались формулой суммы геометрической прогрессии, верной при |q| = < 1, то полученное нами разложение верно при |a| < |z| < ∞, и ряд сходится к в вне круга |z| ≤ |a|.