Оценка устойчивости решения задачи Дирихле. Единственность решения задачи Дирихле
ρ(x)
= div(p(x)∇u2) + q(x)u2 + f(x, t), x ∈ Ω, t > 0
u2(x, 0) = φ(x), x ∈ Ω
u2(x, t) = g(x, t), x ∈ 
, t > 0
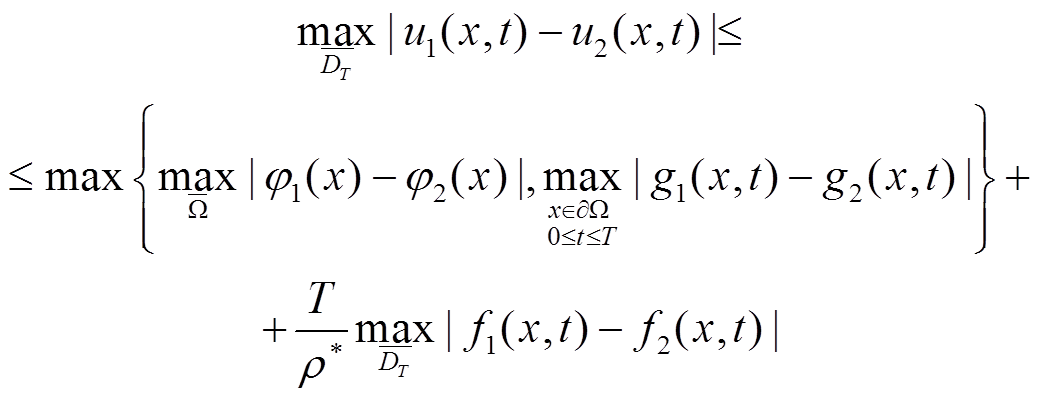
φ1(x) = φ2(x), g1(x, t) = g2(x, t), f1(x, t) = f2(x, t) |
u1(x, t) − u2(x, t) ≡ 0 ⇒u1(x, t) ≡ u2(x, t) |
15/20
