Спектральная плотность сигнала, смещённого во времени

Для прак­ти­че­ских при­ло­же­ний яв­ля­ет­ся важ­ным уста­нов­ле­ние свя­зи меж­ду пре­об­ра­зо­ва­ни­ем сиг­на­ла и со­от­вет­ству­ю­щим это­му пре­об­ра­зо­ва­нию из­ме­не­ни­ем спек­траль­ных ха­рак­те­ри­стик.

Пред­по­ло­жим, что сиг­нал u₁(t) про­из­воль­ной фор­мы, су­ще­ству­ю­щий на ин­тер­ва­ле от t₁ до t₂, име­ет спек­траль­ную плот­ность S₁(jω). Най­дём спек­траль­ную плот­ность это­го же сиг­на­ла при усло­вии его за­держ­ки на ин­тер­вал t₀, на­при­мер пре­об­ра­зо­ва­те­лем, на­зы­ва­е­мым ли­ни­ей за­держ­ки. Функ­ция вре­ме­ни за­дер­жан­но­го сиг­на­ла при со­хра­не­нии его фор­мы за­пи­шет­ся в ви­де:

Спек­траль­ная плот­ность за­дер­жан­но­го сиг­на­ла S₂(jω) оче­вид­но име­ет вид:

Вво­дя но­вую пе­ре­мен­ную ин­те­гри­ро­ва­ния τ = t − t₀, по­лу­чим:

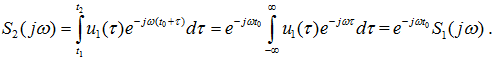
Из это­го со­от­но­ше­ния вид­но, что за­держ­ка во вре­ме­ни сиг­на­ла u₁(t) на ин­тер­вал t₀ при­во­дит к из­ме­не­нию фа­зо­вой ха­рак­те­ри­сти­ки спек­тра S₁(jω) (спек­тра фаз) на ве­ли­чи­ну (−ωt₀). Оче­вид­но, что в об­щем слу­чае при сдви­ге сиг­на­ла во вре­ме­ни на ве­ли­чи­ну (±t₀) его фа­зо­вый спектр из­ме­нит­ся на ве­ли­чи­ну (±ωt₀). Спектр ам­пли­туд это­го сиг­на­ла (мо­дуль спек­траль­ной плот­но­сти) от по­ло­же­ния сиг­на­ла на вре­мен­ной оси не за­ви­сит.