Спектральная плотность сигнала, сжатого во времени

Пусть сиг­нал u₁(t) дли­тель­но­стью τ под­верг­ся сжа­тию во вре­ме­ни в со­от­вет­ствии с ри­сун­ком:

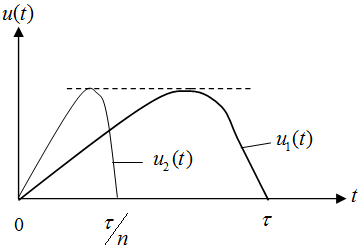
Но­вый сжа­тый сиг­нал u₂(t) свя­зан с ис­ход­ным сиг­на­лом со­от­но­ше­ни­ем:

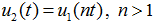
Дли­тель­ность сжа­то­го сиг­на­ла оче­вид­но рав­на τ/n. Опре­де­лим спек­траль­ную плот­ность сжа­то­го сиг­на­ла u₂(t) :

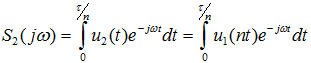
Вво­дя но­вую пе­ре­мен­ную ин­те­гри­ро­ва­ния x = nt, по­лу­ча­ем:

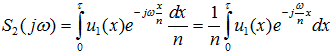
Ин­те­грал в пра­вой ча­сти вы­ра­же­ния (5.6) есть не что иное, как спек­траль­ная плот­ность ис­ход­но­го сиг­на­ла u₁(t) при ча­сто­те 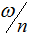, т. е.:

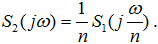
Итак, при сжа­тии сиг­на­ла в n раз на вре­мен­ной оси име­ем:

• умень­ше­ние мо­ду­ля спек­траль­ной плот­но­сти в n раз;
• рас­ши­ре­ние во столь­ко же раз его спек­траль­ных со­став­ля­ю­щих на оси ча­стот.

Оче­вид­но, при рас­ши­ре­нии ис­ход­но­го сиг­на­ла во вре­ме­ни (т. е. при n < 1) име­ют ме­сто об­рат­ные про­цес­сы: суже­ние спек­тра и уве­ли­че­ние мо­ду­ля спек­траль­ной плот­но­сти.

Мож­но так­же по­ка­зать, что дли­тель­ность сиг­на­ла и ши­ри­на его спек­тра ам­пли­туд не мо­гут быть од­но­вре­мен­но огра­ни­че­ны ко­неч­ны­ми ин­тер­ва­ла­ми: ес­ли дли­тель­ность сиг­на­ла огра­ни­че­на, то спектр его не­огра­ни­чен, и, на­обо­рот, сиг­нал с огра­ни­чен­ным спек­тром длит­ся бес­ко­неч­но дол­го. Го­во­рят, что ши­ри­на спек­тра и дли­тель­ность им­пуль­са свя­за­ны со­от­но­ше­ни­ем не­опре­де­лён­но­сти: Δt × Δf = C, где Δt — дли­тель­ность им­пуль­са, а Δf — ши­ри­на спек­тра (прак­ти­че­ская ши­ри­на), C — по­сто­ян­ная, за­ви­ся­щая от фор­мы им­пуль­са (в пер­вом при­бли­же­нии при­ни­ма­ют C = 1).