Импульсная характеристика системы
Импульсной характеристикой стационарной измерительной системы, описываемой оператором T, называют функцию g(t), являющуюся откликом системы на входной сигнал в виде δ-функции:
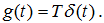
Поскольку в частотной области связь между спектральными плотностями сигналов на входе и выходе и частотной характеристикой системы описывается выражением:
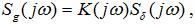
то с учётом:
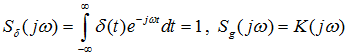
Следовательно,
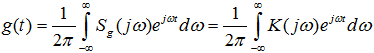
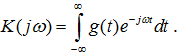
Формулы (7.4) и (7.5) устанавливают принципиально важный факт — частотная характеристика и импульсная характеристика линейной стационарной системы связаны между собой прямым и обратным преобразованиями Фурье. Поэтому, зная функцию K(jω), всегда можно определить импульсную характеристику g(t) наоборот. Таким образом, любую систему можно рассматривать либо во временной области с помощью её импульсной характеристики, либо в частотной области, анализируя K(jω). Следует представлять, что импульсная характеристика, так же как и порождающая её дельта-функция, — результат разумной идеализации. С физической точки зрения импульсная характеристика приближённо отображает реакцию системы на входной импульсный сигнал произвольной формы с единичной площадью при условии, что длительность этого сигнала ≪ характерного временного масштаба системы, например, периода её собственных колебаний.



