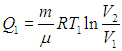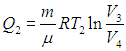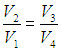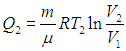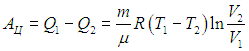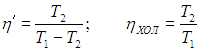5.2. Цикл Карно

Для работы любой тепловой машины по замкнутому циклу необходима внешняя среда, которую условно можно представить себе как два тела — нагреватель, находящийся при температуре Т_mах, и холодильник, находящийся при температуре T_min (T_min < Т_mах). Предполагается, что при контакте с нашей системой температуры нагревателя и холодильника не меняются. При контакте с нагревателем система получает тепло, при контакте с холодильником - отдает его.

В термодинамике существует теорема Карно (рис. 5.2):

Рис. 5.2. Леонар Сади Карно (французский физик и военный инженер)

 

Реализация максимально возможного КПД достигается в так называемом цикле Карно, когда идеальный газ проходит замкнутый цикл, составленный из двух адиабат и двух изотерм (рис. 5.3).

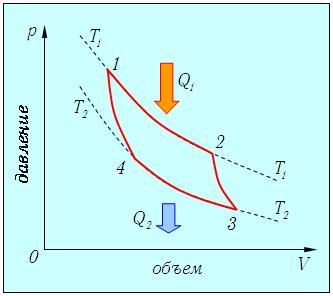
Рис. 5.3. Цикл Карно (обходится по часовой стрелке) — комбинация двух изотерм 1-2, 3-4 и двух адиабат 2-3 и 4-1; теплообмен со средой осуществляется на изотермических участках цикла: на участке 1-2 газ получает теплоту Q₁, а на участке 3-4 отдает теплоту Q₂

Убедимся, что показанный замкнутый процесс действительно имеет КПД, соответствующий формуле (5.5). Температура системы равна T₁ в точках 1, 2 и T₂ в точках 3, 4. Значения остальных термодинамических параметров (р, V) будут иметь в качестве индекса номер соответствующей точки на диаграмме. Нам надо вычислить количества полученной Q₁, и отданной Q₂ теплоты, найти совершенную газом работу А_Ц = Q₁ – Q₂ и определить КПД цикла. Сразу заметим, что на участках 2-3 и 4-1 система не обменивается теплом с внешней средой. Следовательно, теплоту Q₁ газ получает на участке 1-2, а теплоту Q₂ отдает на участке 3-4. Рассмотрим подробнее различные участки цикла.

См. анимацию «Цикл Карно»

Изотерма 1-2. На этом участке газ находится в контакте с нагревателем и происходит изотермическое расширение от объема V₁ до объема V₂. Температура Т₁ не меняется, следовательно, не изменяется внутренняя энергия, а вся полученная теплота расходуется на совершение газом работы:

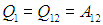
Величину работы газа при изотермическом процессе мы уже вычисляли ранее, так что с учетом формулы (2.13) находим

Адиабата 2-3. Здесь система отсоединяется от нагревателя и не обменивается теплом с внешней средой: Q₂₃ = 0. Газ продолжает расширяться, но уже адиабатно. Работа совершается за счет внутренней энергии газа, и его температура падает до значения Т₂. На этом участке цикла нам нужна информация, доставляемая уравнением адиабаты:

Изотерма 3-4. Система подключается к холодильнику, и газ начинает сжиматься. Внутренняя энергия остается неизменной, над газом совершается работа (А₃₄ < 0), а выделяющееся

тепло

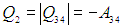
передается холодильнику. Имеем аналогично (5.6)

Адиабата 4-1. Система отключена от внешней среды и продолжает сжиматься изотермически, что приводит к повышению ее температуры до Т₁. В конечном итоге система возвращается в первоначальное состояние. Поскольку точки 4 и 1 лежат на адиабате, получаем связь объемов и температур, аналогичную (5.7):

Из уравнений (5.7) и (5.9) находим отношения объемов

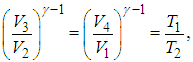
откуда следует, что

Поэтому отдаваемую холодильнику теплоту Q₂ (см. уравнение (5.8)) можно записать как

Используя выражение (5.6) для теплоты, полученной системой, находим совершенную в ходе цикла работу

Из проведенного анализа следует также, что максимальная температура в цикле равна Т_mах = Т₁, а минимальная — Т_min = Т₂. Если разделить (5.12) на (5.6), то немедленно получим выражение (5.5) для КПД цикла Карно, из которого выпадают все параметры, кроме температур холодильника и нагревателя.

Пример 1. Котел тепловой станции работает при температуре около t₁ = 550 °С. Отработанное тепло отводится к реке при температуре около t₂ = 20 °С. Найдем максимально возможный КПД этой станции (рис. 5.4).

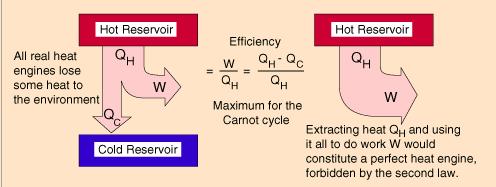
Рис. 5.4. Схема работы тепловой машины Карно

Поскольку в формуле для КПД цикла Карно используются абсолютные температуры, надо перейти от шкалы Цельсия к шкале Кельвина: Т₁ = 550 + 273 = 823 К, Т₂ = 20 + 273 = 293 К. Теперь находим КПД тепловой станции:

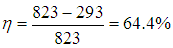
Конечно, реальный КПД станции заметно ниже.

Если цикл Карно осуществить в обратном направлении, то есть против часовой стрелки на рис. 5.2, то для определения эффективности холодильной установки надо использовать формулы (5.3), (5.4) и выражения (5.6), (5.11). Получаем тогда

Печально, но чем ниже температура внешней среды Т₁, тем меньше мы нуждаемся в холодильнике, и тем эффективнее он работает.

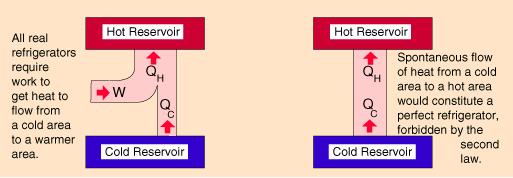
Рис. 5.5. Схема работы холодильной установки

Приведем численный пример. Если кондиционер поддерживает в комнате температуру t₂ = 20 °С, а температура наружного воздуха равна t₁ = 30 °С, то для холодильного коэффициента имеем

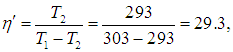
а для КПД холодильника

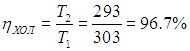
Конечно, на самом деле температура тепловыделяющего элемента больше наружной температуры на 20–30 градусов, так что разность температур может достигать 30–40 градусов, что приводит к значениям

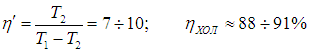
Напомним, что речь идет об идеальных установках, работающих по циклу Карно. Реальный типичный кондиционер потребляет мощность 750 Вт, перекачивая за час около 5 МДж тепловой энергии. Это значит, что за секунду кондиционер совершает работу А = 750 Дж и отнимает у воздуха в комнате теплоту

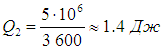
Отсюда находим

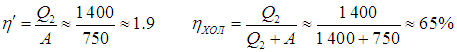
Мы видим, что реальный кондиционер гораздо менее эффективен, нежели идеальный холодильник Карно.

Пример 2. Пусть в домашнем холодильнике поддерживается температура t₂ = –3 °С (Т₂ = 270 К), а температура в кухне равна t₁ = 27 °С (T₁ = 300 К). Пусть далее мотор холодильника потребляет мощность N = 200 Вт. Предполагая, что холодильник работает по циклу Карно и что тепловыделяющий элемент имеет температуру окружающего воздуха, определим мощность потока тепловой энергии, перекачиваемой из камеры холодильника в кухню.

За время t мотор совершит работу

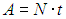
КПД холодильника равен

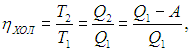
откуда находим количество теплоты, поступающее в кухню в единицу времени:

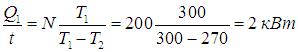
Обратите внимание, что холодильник работает как весьма эффективный обогреватель помещения. Надо только оплачивать потребляемую мотором мощность 200 Вт, а в кухню поступит в 10 раз большая энергия, 90 % которой перекачивается из камеры холодильника (90 % — КПД холодильника в этом примере). Любопытно, что если бы вместо холодильника был включен обогреватель той же мощности, то он нагревал бы помещение в 10 раз слабее.

Наши численные оценки можно рассматривать как пример теплового загрязнения окружающей среды, свойственного технической цивилизации.

 

Дополнительная информация

http://eqworld.ipmnet.ru/ru/library/physics/thermodynamics.htm — Я. де Бур Введение в молекулярную физику и термодинамику, Изд. ИЛ, 1962 г. — стр. 202–205,  ч. 2, гл. 2,  § 10: описан процесс ожижения газа Клода — Гейландта.