2.8. Вращение абсолютно твердого тела

Рассмотрим кинематику движения протяженного тела, размерами которого в условиях рассматриваемой задачи пренебречь нельзя. Тело будем считать недеформируемым, другими словами, — абсолютно твердым.

Под прямой «жестко связанной с телом» понимается такая прямая, расстояние от любой точки которой до любой точки тела остается постоянным при его движении.

Поступательное движение абсолютно твердого тела можно охарактеризовать движением какой-либо точки этого тела, так как при поступательном движении все точки тела движутся с одними и теми же скоростями и ускорениями, а траектории их движения конгруэнтны. Определив движение какой-нибудь из точек твердого тела, мы вместе с тем определим движение всех остальных его точек. Поэтому при описании поступательного движения не возникает новых проблем по сравнению с кинематикой материальной точки. Пример поступательного движения показан на рис. 2.20.

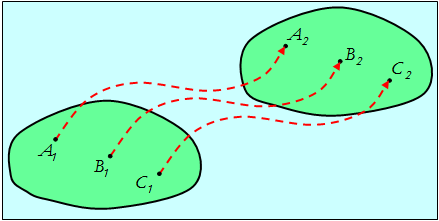
Рис.2.20. Поступательное движение тела

Пример поступательного движения показан на следующем рисунке:

Рис.2.21. Плоское движение тела

Другой важный частный случай движения твердого тела — это движение, при котором две точки тела остаются неподвижными.

Рис.2.22. Вращение твердого тела

При таком движении все точки тела движутся по окружностям, расположенным в плоскостях, перпендикулярных оси вращения. Центры окружностей лежат на оси вращения. При этом ось вращения может находиться и вне тела.

Видео 2.4. Поступательное и вращательное движения.

Угловая скорость, угловое ускорение. При вращении тела вокруг какой-либо оси все его точки описывают окружности различного радиуса и, следовательно, имеют различные перемещения, скорости и ускорения. Тем не менее, можно описать вращательное движение всех точек тела одинаковым образом. Для этого используют иные (по сравнению с материальной точкой) кинематические характеристики движения — угол поворота , угловую скорость , угловое ускорение .

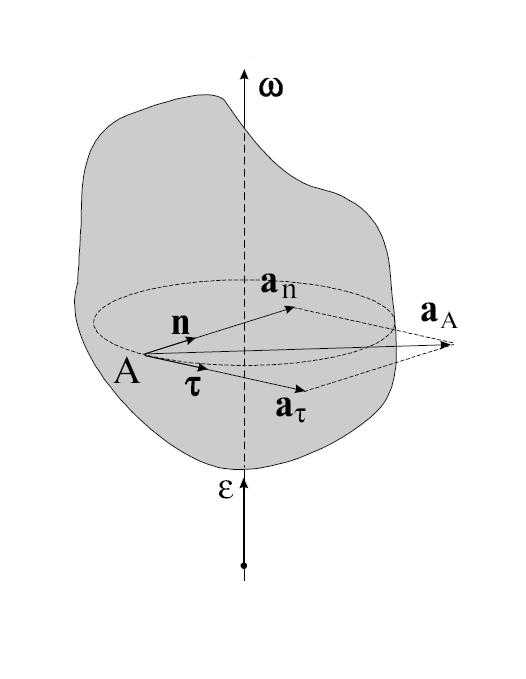
Рис. 2.23. Вектора ускорения точки, движущейся по окружности

Роль перемещения при вращательном движении играет вектор малого поворота , вокруг оси вращения 00' (рис. 2.24.). Он будет одинаков для любой точки абсолютно твердого тела (например, точек 1, 2, 3 ).

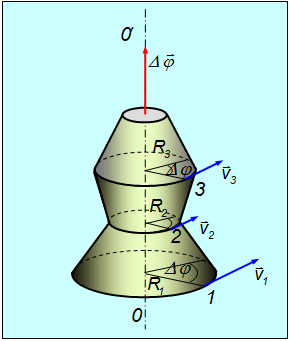
Рис. 2.24. Вращение абсолютно твердого тела вокруг неподвижной оси

Модуль вектора поворота равен величине угла поворота 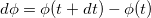причем угол измеряется в радианах.

Направлен вектор бесконечно малого поворота по оси вращения в сторону движения правого винта (буравчика), вращаемого в том же направлении, что и тело.

Видео 2.5. Конечные угловые перемещения — не векторы, так как не складываются по правилу параллелограмма. Бесконечно малые угловые перемещения – векторы.

Векторы, направления которых связаны с правилом буравчика, называют аксиальными (от англ. axis — ось) в отличие от полярных. векторов, которыми мы пользовались ранее. Полярными векторами являются, например, радиус-вектор, вектор скорости, вектор ускорения и вектор силы. Аксиальные векторы называют также псевдовекторами, так как они отличаются от истинных (полярных) векторов своим поведением при операции отражения в зеркале (инверсии или, что то же самое, переходе от правой системы координат к левой). Можно показать (это будет сделано позже), что сложение векторов бесконечно малых поворотов происходит так же как и сложение истинных векторов, то есть по правилу параллелограмма (треугольника). Поэтому, если операция отражения в зеркале не рассматривается, то отличие псевдовекторов от истинных векторов никак не проявляет себя и обходиться с ними можно и нужно как с обычными (истинными) векторами.

Основной единицей измерения величины угловой скорости является рад/с. В печатных изданиях, по причинам никакого отношения к физике не имеющим, нередко пишут 1/с или с^-1, что, строго говоря, неверно. Угол — величина безразмерная, но единицы его измерения различны (градусы, румбы, грады …) и их необходимо указывать, хотя бы во избежание недоразумений.

Видео 2.6. Стробоскопический эффект и его использование для дистанционного измерения угловой скорости вращения.

Угловая скорость 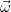как и вектор 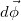, которому она пропорциональна, является аксиальным вектором. При вращении вокруг неподвижной оси угловая скорость не меняет своего направления. При равномерном вращении остается постоянной и ее величина, так что вектор 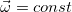. В случае достаточного постоянства во времени величины угловой скорости вращение удобно охарактеризовать его периодом Т :

Слова «достаточного постоянства» означают, очевидно, что за период (время одного оборота) модуль угловой скорости меняется несущественно.

Часто используют также число оборотов в единицу времени

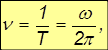
откуда

При этом в технических приложениях (прежде всего, всякого рода двигатели) в качестве единицы времени общепринято брать не секунду, а минуту. То есть угловая скорость вращения 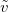указывается в оборотах в минуту. Как легко видеть, связь между (в радианах в секунду) и 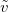(в оборотах в минуту) следующая

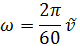
Направление вектора угловой скорости показано на рис. 2.25.

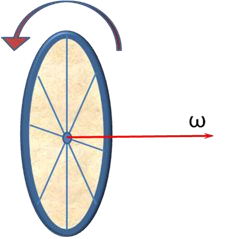
Рис. 2.25. Направление вектора угловой скорости

По аналогии с линейным ускорением вводится угловое ускорение 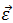как скорость изменения вектора угловой скорости. Угловое ускорение также является аксиальным вектором (псевдовектором).

При вращении вокруг неподвижной оси, в более общем случае при вращении вокруг оси, которая остается параллельной самой себе, вектор угловой скорости также направлен параллельно оси вращения. При возрастании величины угловой скорости |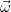| угловое ускорение совпадает с ней по направлению, при убывании — направлено в противоположную сторону. Подчеркнем, что это лишь частный случай неизменности направления оси вращения, в общем случае (вращение вокруг точки) ось вращения сама поворачивается и тогда сказанное выше неверно.

Связь угловых и линейных скоростей и ускорений. Каждая из точек вращающегося тела движется с определенной линейной скоростью , направленной по касательной к соответствующей окружности (см. рис. 19). Пусть материальная точка вращается вокруг оси 00' по окружности радиусом R. За малый промежуток времени она пройдет путь , соответствующий углу поворота . Тогда

Переходя к пределу 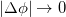, получим выражение для модуля линейной скорости точки вращающегося тела.

Напомним, здесь R — расстояние от рассматриваемой точки тела до оси вращения.

Рис. 2.26.

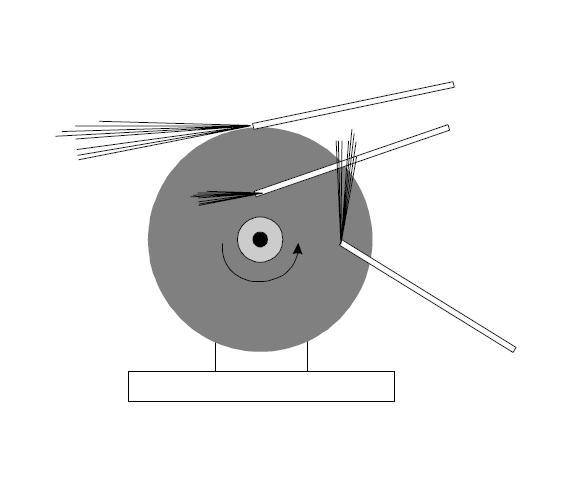
Рис. 2.27. Направление движения искр при заточке инструментов.

Так как нормальное ускорение равно

то с учетом соотношения для угловой и линейной скорости получаем

Нормальное ускорение точек вращающегося твердого тела часто называют центростремительным ускорением.

Дифференцируя по времени выражение для , находим

где — тангенциальное ускорение точки, движущейся по окружности радиусом R.

Таким образом, как тангенциальное, так и нормальное ускорения растут линейно с ростом радиуса R — расстояния от оси вращения. Полное ускорение также линейно зависит от R :

Пример. Найдем линейную скорость и центростремительное ускорение точек, лежащих на земной поверхности на экваторе и на широте Москвы ( = 56°). Мы знаем период вращения Земли вокруг собственной оси Т = 24 часа = 24х60х60 = 86 400 с. Отсюда находится угловая скорость вращения

Средний радиус Земли

Расстояние до оси вращения на широте равно

Отсюда находим линейную скорость

и центростремительное ускорение

На экваторе = 0, cos = 1, следовательно,

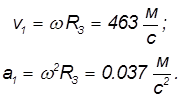
На широте Москвы cos = cos 56° = 0,559 и получаем:

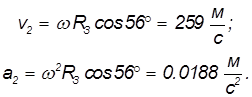
Мы видим, что влияние вращения Земли не столь велико: отношение центростремительного ускорения на экваторе к ускорению свободного падения равно

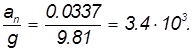
Тем не менее, как мы увидим в дальнейшем, эффекты вращения Земли вполне наблюдаемы.

Связь между векторами линейной и угловой скорости. Полученные выше соотношения между угловой и линейной скоростью записаны для модулей векторов и . Чтобы записать эти соотношения в векторном виде, используем понятие векторного произведения.

Пусть 0z — ось вращения абсолютно твердого тела (рис. 2.28).

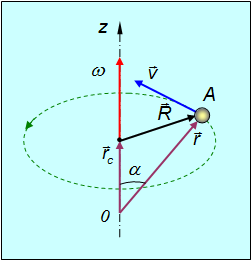
Рис. 2.28. Связь между векторами линейной и угловой скорости

Точка А вращается по окружности радиусом R. R — расстояние от оси вращения до рассматриваемой точки тела. Примем точку 0 за начало координат. Тогда

и так как

то по определению векторного произведения, для всех точек тела

Здесь 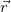— радиус-вектор точки тела, начинающийся в точке О, лежащей в произвольном фиксированном месте, обязательно на оси вращения

Но, с другой стороны

и

Первое слагаемое равно нулю, так как векторное произведение коллинеарных векторов равно нулю. Следовательно,

где вектор R перпендикулярен оси вращения и направлен от нее, а его модуль равен радиусу окружности, по которой движется материальная точка и начинается этот вектор в центре этой окружности.

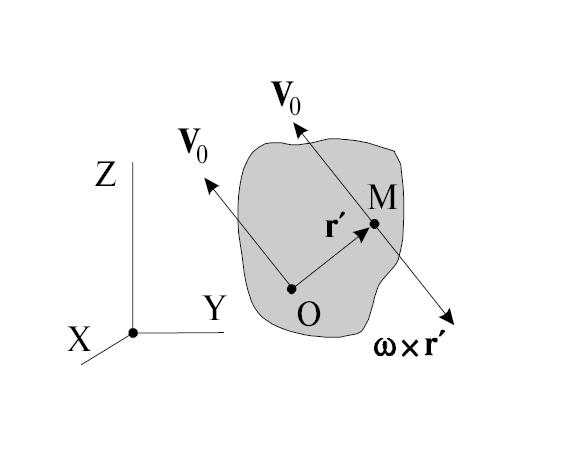
Рис. 2.29. К определению мгновенной оси вращения

Нормальное (центростремительное) ускорение также можно записать в векторной форме:

причем знак «–» показывает, что оно направлено к оси вращения. Дифференцируя соотношение для линейной и угловой скорости по времени, находим для полного ускорения выражение

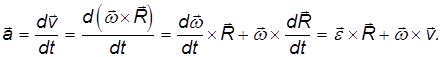
Первое слагаемое направлено по касательной к траектории точки на вращающемся теле и его модуль равен , поскольку

Сравнивая с выражением для тангенциального ускорения, приходим к выводу, что это — вектор тангенциального ускорения

Следовательно, второе слагаемое представляет собой нормальное ускорение этой же точки:

Действительно, оно направлено вдоль радиуса R к оси вращения и его модуль равен

так как

Поэтому данное соотношение для нормального ускорения является другой формой записи ранее полученной формулы.

Дополнительная информация

http://www.plib.ru/library/book/14978.html — Сивухин Д.В. Общий курс физики, том 1, Механика Изд. Наука 1979 г. – стр. 242–243 (§46, п. 7) : обсуждается достаточно трудный для понимания вопрос о векторном характере угловых поворотов твердого тела;

http://www.plib.ru/library/book/14978.html — Сивухин Д.В. Общий курс физики, том 1, Механика Изд. Наука 1979 г. – стр. 233–242 (§45, §46 п.п. 1–6) : мгновенная ось вращения твердого тела, сложение вращений;

http://kvant.mirror1.mccme.ru/1990/02/kinematika_basketbolnogo_brosk.html — журнал «Квант» – кинематика баскетбольного броска (Р. Винокур);

http://kvant.mirror1.mccme.ru/ — журнал «Квант» 2003 г. №6, – стр. 5–11, поле мгновенных скоростей твердого тела (С. Кротов);