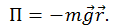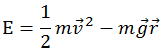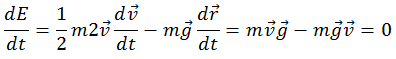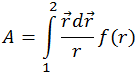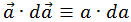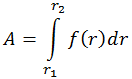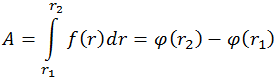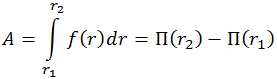4.4. Потенциальная энергия

Выше мы уже получили выражение для работы, совершаемой при растяжении пружины. Рассмотрим следующую систему. Нерастянутая пружина лежит на гладкой горизонтальной плоскости, один ее конец закреплен, а ко второму прикреплен грузик массой m. Начало координатной оси поместим в точку, где находится свободный конец пружины. Мы оттягиваем пружину на расстояние х_max и отпускаем грузик без начальной скорости. Каково движение грузика?

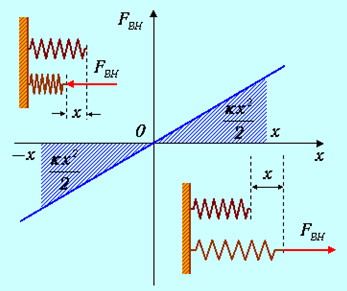
Рис 4.6. Работа при изменении длины пружинки.

В горизонтальной плоскости на грузик действует только упругая сила деформированной пружины, стремящаяся вернуть его к началу координат (положению равновесия). Под действием этой силы грузик приходит в движение. Если его координата в какой-то момент времени равна x, то в этот момент на грузик действует со стороны пружины упругая сила 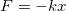. Поэтому уравнение движения грузика имеет вид

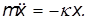
Умножим обе части равенства на скорость грузика

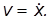
Произведение в левой части можно представить в виде производной

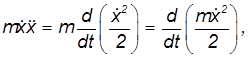
а произведение в правой части — в виде производной

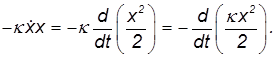
Поэтому уравнение движения грузика можно записать теперь в виде

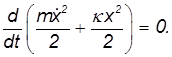
Раз производная выражения в скобках равна нулю, само это выражение не зависит от времени, оно постоянно (сохраняет свое начальное значение):

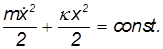
Как бы ни двигался грузик на пружинке, выписанная сумма двух слагаемых не меняется. В первом слагаемом мы узнаем кинетическую энергию грузика, а во втором — работу по растяжению (сжатию) пружины на расстояние х. Совершив эту работу, мы запасаем энергию упругой деформации пружины (ее называют потенциальной энергией). В любой момент времени грузик обладает какой-то кинетической энергией, а пружина — потенциальной.

Значение постоянной интегрирования в выражении для полной механической энергии системы «грузик — пружинка» находим, вспоминая начальные условия: при t = 0 мы отпустили грузик без начальной скорости v(0) = 0 на расстоянии x(0) = х_max от начала координат. Отсюда полная механическая энергия системы будет равна

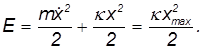
В начальный момент времени кинетическая энергия грузика равна нулю, и полная энергия системы равна той работе, которую мы сначала совершили, растянув пружину на расстояние х_max. Затем груз двигается к началу координат с возрастающей скоростью. В момент прохождения положения равновесия (х = 0) потенциальная энергия пружины равна нулю, следовательно, кинетическая достигает максимума. Грузик проходит положение равновесия, сила упругости меняет знак и начинает его тормозить. Скорость груза обращается в нуль при х = –х_max , когда полная энергия системы снова состоит лишь из потенциальной энергии (на этот раз сжатой) пружины. Далее процесс "перекачки" потенциальной энергии в кинетическую и обратно повторяется.

На этом частном примере мы заметили, что

• сохраняется полная энергия Е системы «грузик-пружинка», равная сумме кинетической энергии К = mv²/2 грузика и потенциальной энергии П = kх²/2 пружинки;
• потенциальная энергия пружины связана с работой по ее растяжению (сжатию): П = А_внеш ;
• силу упругости F = –kх = –F_внеш со стороны деформированной пружины можно получить дифференцированием потенциальной энергии по координате:

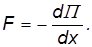
Потенциальное поле сил. Обобщим теперь наш частный случай. Пусть на частицу в каждой точке пространства действует определенная сила F (r,t), зависящая только от положения частицы и, быть может, от времени. Поскольку действующая сила не зависит от движения частицы, мы можем считать ее атрибутом пространства. В этом случае говорят, что в пространстве задано силовое поле. Например, поле тяжести Земли мы можем рассматривать как внешнее силовое поле по отношению к таким телам, движущимся в этом поле, как люди, автомобили, поезда, самолеты, спутники, вода в реках, облака в небе и так далее, по той простой причине, что их движение никак не влияет на характеристики этого поля. Совершенно очевидно, что это обусловлено размерами Земли.

Видео 4.1. Баллистический маятник — двухстадийный процесс демонстрация сохранения импульса на первом этапе и сохранения полной механической энергии на втором этапе.

Среди силовых полей мы выделим потенциальные поля, которые можно описать некоторой скалярной функцией

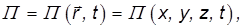
такой, что

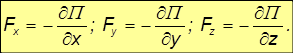
Здесь F_x, F_{y, Fz} проекции силы на направления осей некоторой декартовой системы координат, её разложение по базису имеет вид

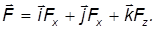
Как будет видно из дальнейшего, связь потенциальной энергии и силы оказывается действительно полезной, когда функция П не зависит от времени. Только этот случай и будет рассматриваться на протяжении всего курса.

Выражение для вектора силы можно записать более компактно. Для этого вводят операцию градиент — своего рода «векторное» дифференцирование функции (не путать с просто дифференцированием вектора, например, по времени):

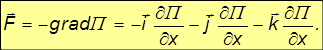
Знак минус, поставленный впереди, к операции «градиент» отношения не имеет и присутствует в выражении для вектора силы ради удобства (см. пример с пружиной выше и текст ниже) Применение операции «градиент» (grad) к скалярному полю (скалярной функции координат) порождает векторное поле. Ясно, что расчеты движения в потенциальных полях должны быть проще хотя бы потому, что вместо трех функций (проекций силы) мы будем иметь дело лишь с одной функцией П(x,y,z)..

Рассмотрим стационарное потенциальное силовое поле (то есть потенциальное поле П(x,y,z), не зависящее явно от времени). Найдем элементарную работу сил поля при перемещении ds:

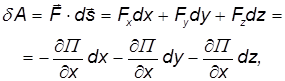
то есть элементарная работа

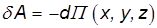
представляется как взятый с обратным знаком полный дифференциал функции П. С другой стороны, поскольку работа равна приращению кинетической энергии тела

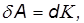
получаем отсюда

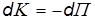
или

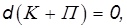
то есть сохраняется сумма

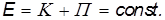
Таким образом, для стационарных потенциальных полей справедливы все выводы, сделанные нами при рассмотрении частного случая грузика на пружинке. Стало быть, скалярная функция П (r), описывающая такое поле, есть не что иное как потенциальная энергия частицы в этом силовом поле.

Консервативные силы. Проинтегрируем полученное соотношение

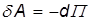
вдоль траектории тела и получим важное свойство стационарных потенциальных полей:

Здесь П₁ = П(r₁) и П₂ = П(r₂) — значения потенциальной энергии в начальной r₁ и конечной r₂ точках перемещения. Соотношение, связывающее работу силы и изменение потенциальной энергии тела, означает, что

Если работа сил поля положительна (частица перемещается под действием сил поля), то ее потенциальная энергия уменьшается: П₂ < П₁. Если же работа сил поля отрицательна (например, внешняя сила вынуждает частицу двигаться против сил поля), то потенциальная энергия частицы увеличивается. Растягивая пружину в нашем примере, мы совершали работу против сил упругости и увеличивали потенциальную энергию системы.

Действительно, в этом случае начальная и конечная точки совпадают, П₂ = П₁ и A₁₂ = 0. Покажем это более детально. Рассмотрим две произвольные точки 1 и 2 и два произвольных пути I и II, их соединяющих (рис. 4.7).

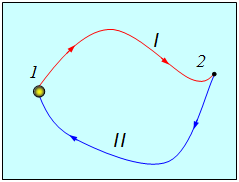
Рис 4.7. Работа при перемещении тела по замкнутому контуру

Пусть поле сил консервативно, то есть работы на этих путях совпадают:

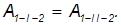
Переместим теперь тело из точки 1 в точку 2 по пути I, а затем — из точки 2 в точку 1 по пути II. Полная совершенная работа по замкнутому контуру равна сумме

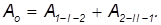
Сравним работы на пути II, проходимом в прямом и обратном направлениях. В каждой точке пути действуют те же силы, но изменение направления движения на обратное приводит к замене ds нa –ds. Таким образом, искомая работа равна

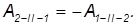
Учитывая полученные соотношения, переписываем выражение для работы по замкнутому контуру в виде

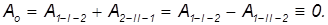
Мы доказали эквивалентность утверждений, что 1) работа консервативных сил не зависит от формы траектории и 2) работа таких сил при обходе замкнутого контура равна нулю.

Итак, стационарное потенциальное поле консервативно. Но верно и обратное: консервативное поле потенциально. Покажем это. Берем произвольную точку r₀ и задаем в этой точке произвольное значение потенциальной энергии П(r₀). При переходе из точки r₀ в любую другую точку r совершается работа A₀₁, не зависящая от пути перехода. Поэтому можно определить функцию П для каждой точки равенством

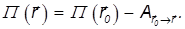
Подчеркнем еще раз: задать функцию П в каждой точке пространства можно лишь вследствие независимости работы от пути. Иначе, проходя из точки r0 в точку r, мы получали бы разные результаты, и функция П была бы неоднозначной (точнее непрерывно бесконечнозначной).

Применим полученное выражение для соседней точки r+dr:

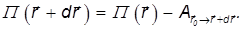
Работу по перемещению из точки r0 в точку r+dr представим как сумму работ по перемещению из r0 в r и из r в r+dr:

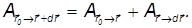
(снова пользуясь независимостью работы от пути). Проведя преобразования, получим

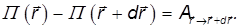
Слева стоит приращение –dП, а справа — элементарная работа 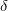A. Полученное соотношение

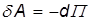
влечет за собой, как мы видели, сохранение величины К+П, то есть введенная нами функция П действительно является потенциальной энергией системы. Таким образом, поле консервативных сил потенциально.

Не следует думать, что все поля в природе потенциальны, а силы — консервативны. Например, силы трения или сопротивления среды всегда направлены против перемещения и, следовательно, имеют одинаковый знак на всей траектории тела. При суммировании элементарных работ по замкнутому пути мы не получим нуля: работа будет зависеть от длины пройденного пути. Значит, эти силы не консервативны.

Произвольная постоянная П(r₀), фигурирующая в формуле для изменения потенциальной энергии, не играет роли, так как физически наблюдаемым является изменение потенциальной энергии, а не ее абсолютное значение. Часто, когда это возможно, в качестве r₀ выбирают бесконечно удаленную точку, и полагают значение потенциальной энергии в ней равной нулю. Но этот выбор не всегда возможен, как демонстрируется в следующем разделе.

Постоянное однородное поле сил тяжести. Вблизи поверхности Земли все тела падают с постоянным ускорением g, направленным к центру планеты. Если мы рассматриваем движение в области, линейные размеры которой много меньше радиуса Земли, земную поверхность можно считать плоской. В этом приближении поле тяжести однородно: силы, действующие на тело, в любой точке имеют одинаковое направление и величину F = mg. Покажем потенциальность поля силы тяжести у поверхности Земли (рис. 4.8).

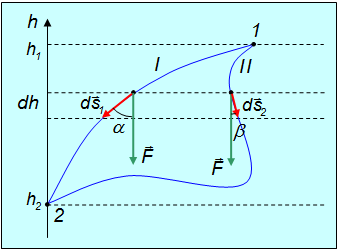
Рис. 4.8. Нахождение потенциальной энергии поля сил тяжести

Элементарная работа при перемещении ds равна

где –dh — проекция перемещения на направление действия силы, то есть dh — изменение высоты тела. Полная работа при перемещении тела из точки 1 в точку 2 равна

Таким образом, в поле сил тяжести работа не зависит от пути, по которому движется частица, а определяется только начальным и конечным положениями частицы в пространстве. Соответственно, потенциальная энергия в поле сил тяжести находится в соответствии с общим рецептом как

Если отсчитывать высоту от поверхности Земли, приписав при этом точке на поверхности нулевую потенциальную энергию П(h₀ = 0) = 0, для произвольной высоты h получим хорошо знакомую формулу

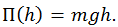
Или в векторном виде

(4.4.1)

В последней формуле радиус вектор 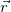начинается в любой точке лежащей на поверхности Земли, потенциальная энергия на поверхности Земли, как и ранее, принята равной нулю.

Пример. Исходя из уравнений движения, показать сохранение полной энергии тела, движущегося в однородном поле силы тяжести.

Решение. Учитывая (4.4.1), запишем полную механическую энергию тела в виде

(4.4.2)

Сохранение во времени некоторой величины означает, что полная производная по времени от этой величины в любой момент времени равна нулю. И обратно, если полная производная по времени от некоторой величины равна нулю тождественно (в любой момент времени), то эта величина сохраняется. Вычислим полную производную по времени механической энергии из (4.4.2):

(4.4.3)

При получении (4.4.3) было учтено, что 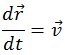и, согласно уравнению движения, ускорение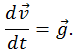

Видео 4.2. Маятник Галилея — демонстрация сохранения полной механической энергии при движении в однородном поле тяжести.

Поле центральных сил

Другой пример. Вычислим работу произвольной центральной стационарной силы при перемещении её точки приложения из некоторой произвольной точки пространства 1, находящейся на расстоянии r₁ до центра поля, в некоторую произвольную точку 2, находящуюся на расстоянии r₂ от центра поля. Воспроизведенные ниже выкладки показывают, что траектория перемещения точки приложения силы может быть любой — результат не зависит от её формы.

Общий вид центральной силы следующий

(4.4.4)

Здесь радиус-вектор 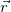начинается в центре поля. Примерами могут служить поле точечного электрического заряда, находящегося в начале координат, или гравитационное поле сферически симметричного объекта с центром в начале координат. Подставив (4.4.4) в общее определение работы, получаем:

(4.4.5)

Криволинейный интеграл вида (4.4.5) легко превращается в обычный интеграл с помощью весьма полезного тождества (4.4.6) ниже. Дифференцируя определение квадрата модуля вектора

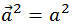
и сокращая на двойку имеем для любого вектора:(4.4.6)

(4.4.6)

То есть, скалярное произведение вектора на его приращение равно произведению модуля этого вектора на приращение его модуля. Заменяя в (4.4.5) скалярное произведение 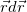на обычное произведение rdr и сокращая на r, получаем

(4.4.7)

Если функция φ(r) есть первообразная для f(r), то окончательно имеем:

(4.4.8)

Из формулы (4.4.8) видно, что величина работы определяется только положением начальной и конечной точек и действительно не зависит от формы траектории перемещения точки приложения силы. Часто говорят короче: работа не зависит от пути. Работа получилась равной приращению первообразной φ(r), поэтому отождествлять её с потенциальной энергией неудобно: получится, что при совершении положительной работы растет и функция f(r). Потенциальная энергия вводится как П = –φ(r), тогда, при совершении положительной работы, потенциальная энергия убывает и можно говорить и так: работа совершается за счет убыли потенциальной энергии тела в силовом поле. Тогда

(4.4.9)

Вычисление интеграла с помощью тождества (4.4.6) иллюстрирует следующий рисунок

Рис. 4.8. Работа центральной силы

Положив потенциальную энергию в точке с радиус-вектором 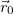равной 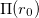, для её значения в произвольной точке с радиус-вектором 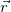, получим

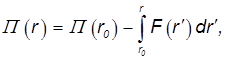
Покажем, что операция «градиент», примененная к потенциальной энергии П(r), действительно дает нам поле центральных сил, направленных по радиус-вектору 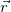и с модулем F(r). Берем производную от П(r) по координате x как производную сложной функции:

Производная по r вычисляется без труда из формулы для потенциальной энергии:

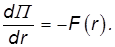
Производная r по x равна

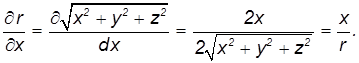
Таким образом,

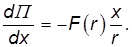
Аналогичные выражения получатся при дифференцировании по координатам y, z. В итоге

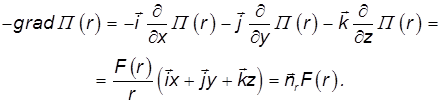
Мы убедились, что исходное центральное поле сил восстанавливается по функции потенциальной энергии:

Рис.4.9. Потенциал гравитационного поля Земли.

Говоря о центральных силах, мы также используем некоторую абстракцию. Что означает силовой центр, к которому (или от которого) направлено поле сил? Мы предполагаем, что центр неподвижен, но реально он образован какими-то физическими телами — зарядами в случае электрического поля, массами — в случае гравитационного. Просто при определенных условиях движением центра можно пренебречь. Скажем, изучая движение спутника вокруг Земли, мы, строго говоря, должны учесть, что спутник и Земля движутся вокруг общего центра масс. Но масса Земли намного превышает массу спутника, центр масс системы практически совпадает с центром Земли, и ее можно считать неподвижным центром гравитационного поля.

Рис.4.10. Зависимость формы траектории от начальной скорости тела.

Если же такого допущения сделать нельзя, то рассматривают силы взаимодействия между телами. Когда силы направлены вдоль линии, соединяющей тела, а их величина зависит только от взаимного расстояния

мы имеем дело с аналогом центральных сил. Здесь тоже можно ввести потенциальную энергию взаимодействия тел между собой П(r₁₂), так что сила F₁₂ между телами 1 и 2 удовлетворяет соотношению

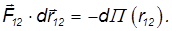
Дополнительная информация

http://kvant.mirror1.mccme.ru/pdf/1998/06/kv0698kaganov.pdf — Журнал «Квант» – применение законов сохранения физических величин для объяснения разнообразных физических явлений (М. Каганов);

http://ilib.mirror1.mccme.ru/djvu/bib-kvant/kvant_70.djvu — Стасенко А.Л. Физика полета, Библиотечка Квант, выпуск 70, стр. 88–98 – энергетика космического полета;

http://vivovoco.rsl.ru/quantum/2001.01/PRKT_1_01.PDF — Приложение к журналу «Квант» – использование законов сохранения в задачах о столкновении частиц (А. Овчинников, В. Плис).